Question

An elevator is descending with uniform acceleration. To measure the acceleration, a person in the elevator drops a coin at the moment the elevator starts. The coin is $6ft$ above the floor of the elevator at the time it is dropped. The person observes that the coin strikes the floor in $1$ second. Calculate from these data the acceleration of the elevator.

Answer 1

In this question, we need to determine the acceleration of the elevator while satisfying the given conditions in the questions as well. For this, we will use the lift as the frame of reference and apply Newton's laws of motion for the same.

Complete step by step answer:
Let initial velocity of the coin and elevator are ${u_c}$ and ${u_e}$ respectively since the person drops the coin at same time when elevator start so, initially, ${u_c}$ and ${u_e}$
Let the elevator and the coin travel a distance ${s_e}$ and ${s_c}$ respectively from
$t = 0$ and $t = t$ i.e. in time t.

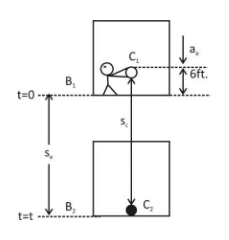
Now, by using the second equation of motion i.e. $s = ut + \dfrac{1}{2}a{t^2}$.
Applying this equation for elevator with respect to coin so,
${S_{ec}} = {u_{ec}} \times t + \dfrac{1}{2}{a_{ec}} \times {t^2}........\left( i \right)$
Where, ${S_{ec}}$ is the displacement of the elevator with respect to coin in time t.
Also,
$\Rightarrow {S_{ec}} = {s_e} - {s_c} \\\ \Rightarrow = {s_e} - \left( {{s_e} + 6} \right) \\\ \Rightarrow = - 6 \\\$
Also, ${u_{ec}} =$initial velocity of elevator with respect to coin so, ${u_{ec}} = {u_e} - {u_c} = 0 - 0 = 0$
Also, ${a_{ec}} =$acceleration of elevator with respect to coin
So, ${a_{ec}} = {a_e} - {a_c}$
Because the coin is dropped so acceleration of coin with respect gravitational acceleration.
So, ${a_c} = g = 32.2$ feet per second [in FPS system]
Now putting all values in equation (i), we get

$$\Rightarrow \- 6 = 0 + \dfrac{1}{2} \times \left( {{a_e} - {a_c}} \right) \times {\left( t \right)^2} \\\ \Rightarrow \left( {{a_e} - {a_c}} \right) \times {\left( t \right)^2} = - 12 \\\$$

Here it is given that in $t = 1s$the elevator descend ${B_1}$to ${B_2}$and the coin from ${C_1}$ to ${C_2}$ so,

$$\left( {{a_e} - {a_c}} \right) \times {\left( t \right)^2} = - 12 \\\ \Rightarrow \left( {{a_e} - {a_c}} \right) \times 1 = - 12 \\\ \Rightarrow {a_e} - 32.2 = - 12 \\\ \Rightarrow {a_e} = - 12 + 32.2 \\\ \Rightarrow = 20.2{\text{ ft/se}}{{\text{c}}^2} \\\$$

Hence, the acceleration of the lift is 20.2 feet per square second (in FPS).

Note: To study the equation of motion relative to another frame replace all variables relative to that frame of observation. For example,
${{\text{x}}_{{\text{AB}}}}{\text{ = }}{{\text{x}}_{\text{A}}}{\text{ - }}{{\text{x}}_{\text{B}}}$
${x_A} \to$ Measurement of physical quality x in the frame of a with respect to ground.
${x_B} \to$ Measurement of physical quantity x in the frame of B with respect to ground and
${x_{AB}} \to$ Measurement of physical quantity x in the frame of A with respect to frame of B. In the FPS measurement system the value of gravitational acceleration is $g = 32.2ft/{s^2}$.