Question

An elevator has a mass of $1000kg$. What is the tension force on its cables when it is stationary?

Answer 1

The tension force is defined as the force that is transmitted through a rope, string or wire when pulled by forces acting from opposite sides. At the atomic level, when atoms are pulled apart from each other and gain potential energy with a restoring force still existing, then the restoring force creates tension.

Complete step by step answer:

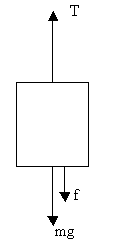
We know that the equation of the force for a stationary lift is:
$T = mg + ma.........(1)$
Now, since the lift is in a stationary position. So, the velocity $v = 0\dfrac{m}{s}$.
Since the velocity is $v = 0\dfrac{m}{s}$, so the acceleration is also $a = 0\dfrac{m}{{{s^2}}}$.
So, the equation (1) becomes,
$T = mg + m(0)$
$T = mg......(2)$
In the question we are given mass $m = 1000kg$ and we also know that the acceleration due to gravity on the earth is $g = 9.81\dfrac{N}{{kg}}$
On putting the values of $m$ and $g$ in equation (2), we get,
$T = 9.81 \times 1000$
$T = 9810N$
So, the tension force on the cables of the lift when it is stationary is $T = 9810N$.

Additional information: The tension force is a centripetal force. Centripetal force is a force which keeps an object rotating on a circular path and this force acts towards the centre. Since, the tension force acts towards the centre, so the tension is a centripetal force.

Note: The value of acceleration due to gravity $g$ varies from place to place. For example, the value of $g$ on earth is $9.81\dfrac{N}{{kg}}$ whereas the value of g on moon is $1.625\dfrac{N}{{kg}}$. In this question, since it was not given to us where the stationary lift is present, so we assumed it to be present on earth and thus, we took the value of acceleration due to gravity as $9.81\dfrac{N}{{kg}}$.