Question

An elevator accelerates upward at a constant rate. A uniform string of length $\;L\;$and mass$M$supports a small block of mass$M$that hangs from the ceiling of the elevator. The tension at distance$l$from the ceiling is$T$. The acceleration of the elevator is
A. $\dfrac{T}{{M + m - \dfrac{{ml}}{L}}} - g$
B. $\dfrac{T}{{2M + m - \dfrac{{ml}}{L}}} - g$
C. $\dfrac{T}{{M + \dfrac{{ml}}{L}}} - g$
D. $\dfrac{T}{{2M - m + \dfrac{{ml}}{L}}} - g$

Answer 1

Here the elevator moves with a constant acceleration upwards. The elevator consists of a small block and a string inside it. Therefore the string and the block also move with the same constant acceleration. They have said that a small part of the string with length $l$ has tension $T$. We need to find out the equation of motion of both the parts of the string in order to find the acceleration of the elevator.

Complete step by step solution:

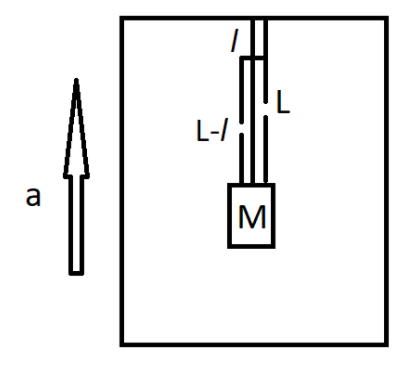
First, we need to find the equation of motion of the lower part. That is the part of the string whose length is $L - l$along with the small block of the mass $M$
We know the total mass of the string is $m$.
The mass of the string of length $L - l$ is given by,
${m_{L - l}} = \dfrac{m}{L}(L - l)$
Here,${m_{L - l}}$ is the mass of the part of the string whose length is $L - l$
$m$ is the total mass of the string inside the elevator.
$L$ is the total length of the string inside the elevator.
We know the equation of motion,
$T - mg = ma$
We are using $T$ in the place of a force because tension is a kind of force that acts on the string. We can draw the free body diagram of above mentioned lower part as

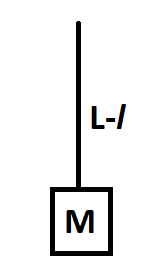
The mass of the part of the string whose length is $L - l$ is ${m_{L - l}} = \dfrac{m}{L}(L - l)$. We also know the mass of the small block is$M$.
Substituting this in the equation of motion,
$T - \dfrac{m}{L}(L - l)g - Mg = \left[ {\dfrac{m}{L}(L - l) + M} \right]a$
Rearranging the above equation to find acceleration we get,
\dfrac{{T - \left[ {\dfrac{m}{L}(L - l) + M} \right]g}}{{\dfrac{m}{L}(L - l) + M}}$$$$ = a
If we expand and write the above equation we get,
$\dfrac{T}{{\dfrac{m}{L}(L - l) + M}} - g = a$
$\dfrac{T}{{M + m - \dfrac{{ml}}{L}}} - g = a$
Therefore the correct option is A.

Note:
Note that we have found the acceleration only for the lower part and not for the elevator. But we can say that the elevator will also have the same acceleration because the string is inside the elevator therefore both string and the elevator will have the same acceleration.