Question

An element crystallizes in bcc structure. The edge length of its unit cell is 288 pm. If the density of the crystal is 7.2 g $cm ^{- 3}$. what is the atomic mass $\;\left( {in{\text{ }}g/mol} \right)$ of the element?
A. 51.8
B. 103.6
C. 25.9
D. 207.2

Answer 1

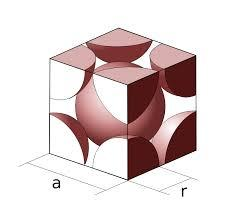
Body-centered cubic unit cell is one kind of cubic lattice. In this cubic lattice each unit cell contains one atom at its body center. And contains one atom at the eight corners of the unit cell.

Formula used: Density = $\dfrac{{(M \times z)}}{{(N \times {a^3})}}$= $\dfrac{{(molecular{\text{ }}weight){\text{ (}}number{\text{ }}of{\text{ }}atoms{\text{ }}per{\text{ }}cell){\text{ }}}}{{{{(edge{\text{ }}length)}^3}{\text{ (}}Avogadro{\text{ }}number)}}$
Complete step by step answer:
The structure is shown below,

We know that,
Density = (mass)/(volume)
Applying this concept for calculating the density of the unite cell, we get,
Density = $\dfrac{{(M \times z)}}{{(N \times {a^3})}}$
= $\dfrac{{(molecular{\text{ }}weight){\text{ (}}number{\text{ }}of{\text{ }}atoms{\text{ }}per{\text{ }}cell){\text{ }}}}{{{{(edge{\text{ }}length)}^3}{\text{ (}}Avogadro{\text{ }}number)}}$
= $7.2 = \dfrac{{M \times 2}}{{{{(288 \times {{10}^{10}})}^3} \times 6.022 \times {{10}^{23}}}}$
Hence,

$$7.2 = \dfrac{{M \times 2}}{{{{(288 \times {{10}^{10}})}^3} \times 6.022 \times {{10}^{23}}}} \\\ M = \dfrac{{7.2 \times {{(288 \times {{10}^{10}})}^3} \times 6.022 \times {{10}^{23}}}}{2} \\\ M = 51.77 \\\$$

Therefore, the molecular weight of the element is $51.77gm/mol$.

Additional information:
In the B.C.C the closest distance between two atoms in the unit lattice is$\dfrac{{\sqrt {\text{3}} a}}{2}$. Where a is the edge length of the unit lattice.
Now according to this formula $\dfrac{{\sqrt {\text{3}} a}}{{\text{2}}}{\text{ = 173pm}}$
Therefore, the edge length is,

$$\dfrac{{\sqrt {{\text{3a}}} }}{{\text{2}}}{\text{ = 173pm}} \\\ {\text{a = }}\dfrac{{{{2 \times 173}}}}{{\sqrt {\text{3}} }} \\\ {\text{a = 200pm}} \\\$$

Note: The contribution of each corner atoms is ${\dfrac{{\text{1}}}{{\text{8}}}^{{\text{th}}}}$ of a total atom. So, the contribution of all eight atoms is, $\dfrac{{\text{1}}}{{\text{8}}} \times 8 = 1$.
For the body center atoms, the contribution of that atom is a total of a total atom.
Total number of atoms is 2 in a B.C.C lattice.