Solveeit Logo
Login

Question

Question: An electron projected with a velocity \(v={{v}_{0}}\hat{i}\) in the electric field \(E={{\bar{E}}_{0...

An electron projected with a velocity v=v0i^v={{v}_{0}}\hat{i} in the electric field E=Eˉ0jE={{\bar{E}}_{0}}j . Trace the path followed by the electron E0.{{E}_{0.}}.
A. Parabola
B. Circle
C. Straight line in + y-direction
D. Straight line in- y-direction

Explanation

Solution

when a particle is accelerated with a certain velocity in the direction perpendicular to the external electric field certain charge is gained by the particle. This charge is due to the developed magnetic field perpendicular to the direction of the applied electric field. Hypothetically, the electric and the magnetic fields can never stand alone.

Complete step by step answer:
When we see the condition mentioned in the question it says that a particle is projected in an electric field (V0{{V}_{0}}) in the jj direction which is along the y-axis in such a way that it is moving with a velocity V0{{V}_{0}} in vector ii direction which is along. This can be described graphically from the following representation.

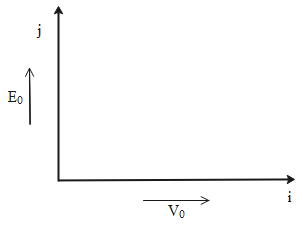
From the graph, we can say that the particle is moving in the direction perpendicular to a perpendicular external electric field.
The acceleration of the particle will depend on the mass of the particle projected on the external electric field and the charge produced on the particle due to the externally applied field.
The acceleration of the electron will be −eEmj^-\dfrac{eE}{m}\hat{j}
The motion of such a particle is analogous to the mass on the particle which is projected with a velocity V0{{V}_{0}} with the gravity acting on the particle which is in the vertical direction.
So, the particle will trace along a parabolic path in the x-y plane.

So, the correct answer is “Option A”.

Note: The electric and the magnetic field cannot stand alone; they recreate the other component perpendicular to them. The motion of a partial perpendicular to the electric field and along the direction of the virtual magnetic field which is developed by the electric field is always influenced by the electric field, the mass of the particle and the vertically applied acceleration due to gravity.