Question

An electron enters a parallel plate capacitor with horizontal speed $\mu$ and is found to deflect by an angle $\theta$ on leaving the capacitor as shown. It is found that $\tan \theta = 0.4$ and gravity is negligible. If the initial horizontal speed is doubled, then tangent will be.

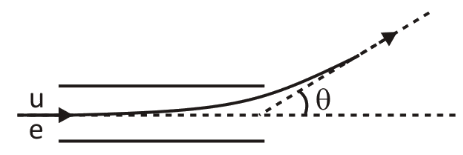
A. $0.1$
B. $0.2$
C. $0.8$
D. $1.6$

Answer 1

First of all, we will draw the schematic diagram, showing the component of the velocity of the electron. After that we will find the final velocity along the vertical direction. Lastly, we will find the tangent to obtain a relation between the tangent of the angle and the initial velocity.

Formula used:
The formula which gives the relation between the final velocity, initial velocity and the acceleration is as follows:
$v = u + at$ …… (1)
Where,
$v$ indicates final velocity.
$u$ indicates initial velocity.
$a$ indicates acceleration.
$t$ indicates time required.
Again, we know,
$t = \dfrac{d}{v}$ …… (2)
$t$ indicates time required.
$d$ indicates displacement.
$v$ indicates velocity.

Complete step by step answer:
In the given question, we are supplied with the following data:
There is an electron which passes through a parallel plate capacitor. The horizontal speed of the electron is $\mu$. The electron is deflected by an angle $\theta$ on leaving the capacitor. The tangent of the angle is found to be $0.4$.The initial horizontal speed is then doubled. We are asked to find the tangent of the angle by which the electron will be deflected.

To begin with, we will draw the diagram, which shows all the components of the velocity.

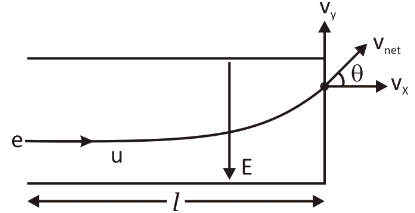
In the diagram, it can be clearly seen that the electric field is directed downwards. The horizontal displacement is labelled as $l$. The horizontal component of the velocity is labelled as ${v_{\text{x}}}$ while the vertical component is labelled as ${v_{\text{y}}}$.

Now, we will use equation (2) for the horizontal case and we get:
t = \dfrac{d}{v} \\\ \Rightarrow t = \dfrac{l}{u} \\\
Again, we know that the acceleration of a charged particle is given as:
$a = \dfrac{{eE}}{m}$
Where,
$e$ indicates the charge of the electron.
$E$ indicates the magnitude of the electric field.
$m$ indicates the mass of the electron.

Now, we use the equation (1) for the vertical case and we get:
{v_{\text{y}}} = {u_{\text{y}}} + at \\\ \Rightarrow {v_{\text{y}}} = 0 + \dfrac{{eE}}{m} \times \dfrac{l}{u} \\\ \Rightarrow {v_{\text{y}}} = \dfrac{{eE}}{m} \times \dfrac{l}{u} \\\
However, the horizontal component of the velocity remains the same and it equals $u$.
So,
\tan \theta = \dfrac{{{v_{\text{y}}}}}{{{v_{\text{x}}}}} \\\ \Rightarrow \tan \theta = \dfrac{{\dfrac{{eE}}{m} \times \dfrac{l}{u}}}{u} \\\ \Rightarrow \tan \theta = \dfrac{{eEl}}{{m{u^2}}} \\\
All the terms in the above equation are constant except $u$. So, we can write the above equation as:
$\tan \theta \propto \dfrac{1}{{{u^2}}}$ …… (3)
From the relation (3), it can be said that when velocity is doubled, then $\tan \theta$ becomes one-fourth.
\Rightarrow \tan \theta = \dfrac{{0.4}}{4} \\\ \therefore\tan \theta = 0.1 \\\
Hence, the tangent of the angle by which the electron will be deflected is $0.1$.

The correct option is A.

Note: While solving the problem, it is important to remember that the initial velocity along the vertical direction is zero, as the electron was moving along the horizontal direction. It is important to note that in both the cases, the horizontal displacement remains the same. However, the angle of deflection changes.