Question

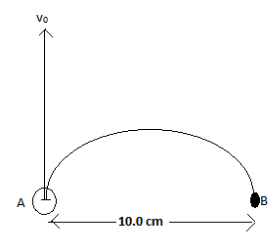
An electron at a point A in figure has a speed ${v_0} = 1.41 \times {10^6}\,{\text{m/s}}$. Find the magnitude and direction of the magnetic field that will cause the electron to follow the semicircular path from A to B.

Answer 1

Use equation for magnetic force and centripetal force in balanced position of electron in its travel. Use Fleming’s left hand rule to determine the direction of the magnetic field.

Formulae used:
The expression for the magnetic force ${F_B}$ on an electron in the magnetic field is
$\Rightarrow{F_B} = qvB$
Here, $q$ is the charge on the electron, $v$ is the speed of the electron and $B$ is the magnetic field.
The expression for the centripetal force ${F_C}$ on an object in circular motion is
$\Rightarrow{F_C} = \dfrac{{m{v^2}}}{R}$
Here, $m$ is the mass of the object, $v$ is the velocity of the object and $R$ is the radius of the circular path.

Complete step by step answer:
An electron is moving in a magnetic field with a speed ${v_0} = 1.41 \times {10^6}\,{\text{m/s}}$.We need the electron to follow the semicircular path from point A to B.

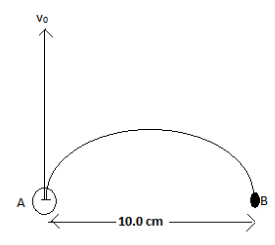
From the above figure, it can be seen that the diameter of the semicircular path is ${\text{10}}{\text{.0 cm}}$. Hence, the radius $R$ of the semicircular path will be
$\Rightarrow R = \dfrac{{{\text{10}}{\text{.0 cm}}}}{2} = {\text{5}}{\text{.0 cm}}$.
The magnetic force ${F_B}$ on the electron in the semicircular path is balanced by the centripetal force ${F_C}$ on the electron. Hence, these two forces must be equal.
$\Rightarrow {F_B} = {F_C}$
Substitute $q{v_0}B$ for ${F_B}$ and $\dfrac{{mv_0^2}}{R}$ for ${F_C}$ in the above equation.
$\Rightarrow q{v_0}B = \dfrac{{mv_0^2}}{R}$
$\Rightarrow qB = \dfrac{{m{v_0}}}{R}$
Here, $m$ is the mass of the electron and $q$ is the charge of the electron.
Rearrange the above equation for the magnetic field $B$.
$\Rightarrow B = \dfrac{{m{v_0}}}{{qR}}$
Substitute $9.1 \times {10^{ - 31}}\,{\text{kg}}$ for $m$, $1.41 \times {10^6}\,{\text{m/s}}$ for ${v_0}$, $1.6 \times {10^{ - 19}}\,{\text{C}}$ for $q$ and $5.00\,{\text{cm}}$ for $R$ in the above equation.
$\Rightarrow B = \dfrac{{\left( {9.1 \times {{10}^{ - 31}}\,{\text{kg}}} \right)\left( {1.41 \times {{10}^6}\,{\text{m/s}}} \right)}}{{\left( {1.6 \times {{10}^{ - 19}}\,{\text{C}}} \right)\left( {5.00\,{\text{cm}}} \right)}}$
$\Rightarrow B = \dfrac{{\left( {9.1 \times {{10}^{ - 31}}\,{\text{kg}}} \right)\left( {1.41 \times {{10}^6}\,{\text{m/s}}} \right)}}{{\left( {1.6 \times {{10}^{ - 19}}\,{\text{C}}} \right)\left[ {\left( {5.00\,{\text{cm}}} \right)\left( {\dfrac{{{{10}^{ - 2}}{\text{ m}}}}{{1\,{\text{cm}}}}} \right)} \right]}}$
$\Rightarrow B = 1.60 \times {10^{ - 4}}\,{\text{T}}$
Hence, the magnetic field on the electron is $1.60 \times {10^{ - 4}}\,{\text{T}}$.
Now, determine the direction of the magnetic field using Fleming’s left hand rule.According to Fleming’s left hand rule, when the forefinger, the middle finger and the thumb are held perpendicular to each other and if the forefinger represents the direction of magnetic field and the thumb represents the direction of magnetic force then the middle finger represents the direction of the electric current.The direction of the magnetic force at the initial point A should be towards right in order to move the electron in a semicircular path.Then according to Fleming’s left hand rule, the direction of the magnetic field should be inward for the electron to follow the same path.

Hence, the magnetic field is $1.60 \times {10^{ - 4}}\,{\text{T}}$ in the inward direction.

Note: Don’t forget to convert the unit of the radius of the semicircular path from centimeter to meter in order to have all the physical quantities in the SI system of units.