Question

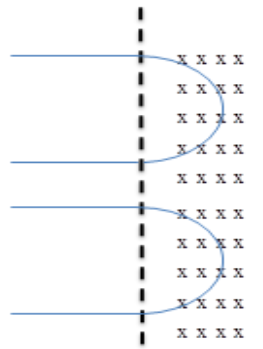
An electron and a proton are moving on straight parallel paths with the same velocity. They enter a semi- infinite region of uniform magnetic field perpendicular to the velocity. Which of the following statement(s) is or are true?
A). They will never come out of the magnetic field region.
B). They will come out travelling along parallel paths.
C). They will come out at the same time.
D). They will come out at different times.

Answer 1

Hint- Since the magnetic force is perpendicular to the direction of travel, a charged particle follows a curved path in a magnetic field.

Complete step-by-step solution -
The magnetic force supplies the centripetal force ${F_c} = \dfrac{{m{v^2}}}{r}$. Noting that the velocity is perpendicular to the magnetic field, the magnitude of the magnetic force is reduced to F=qvB. Because the magnetic force F supplies the centripetal force ${F_c}$ , we have,
$qvB = \dfrac{{m{v^2}}}{r}$
Solving for r yields
$r = \dfrac{{mv}}{{qB}}$
Here, r is the radius of curvature of the path of the charged particle of mass m and charge q, moving at a speed v that is perpendicular to a magnetic field of strength B. The time to go around the circular path is known as the duration that is equal to the distance traveled (speed-divided by circumference). Now we can derive the time period of motion as
$T = \dfrac{{2\pi r}}{v}$

Substituting the value of r in the above equation
$T = \dfrac{{2\pi }}{v} \times \dfrac{{mv}}{{qB}} \\\ T = \dfrac{{2\pi m}}{{qB}} \\\$
Radius of the proton and time period of the proton
${R_p} = \dfrac{{{m_p}V}}{{{q_b}B}}$ ; ${T_p} = \dfrac{{2\pi {m_p}}}{{{q_p}B}}$
Similarly radius and time period of electron
${R_e} = \dfrac{{{m_e}V}}{{{q_e}B}}$ ; ${T_e} = \dfrac{{2\pi {m_e}}}{{{q_e}B}}$
As the mass of the proton is greater than the mass of the electron, therefore the radius of curvature of the proton is greater than the radius of curvature of the electron. And the time period of the proton is greater than the time period of the electron.
And both will come out parallel.
Hence, the correct option is C and D.

Note- If the velocity is not perpendicular to the magnetic field, then we can compare each component of the velocity separately with the magnetic field. As we know that when the velocity of the charge particle is perpendicular to the direction of magnetic field; a force is acted on the charge particle which is perpendicular to both velocity and the field.