Question

An electrician has to repair an electric fault on an electric pole of height $10{\text{m}}$. He needs to reach a point ${\text{3}}{\text{.1m}}$ below the top of the pole to undertake the repair work. What should be the length of the ladder that he should use which were inclined at an angle of $60^\circ$ to the horizontal, would enable him to reach the required position? Give your answer correctly to the nearest meter. Take $\sqrt 3 = 1.73$.

Answer 1

Here, we will use the concept of trigonometry by drawing a triangle from the given information. Where a pole is standing from the point which is our perpendicular of the triangle. Also, the base of the triangle will be the distance of the ladder foot from the pole and the Hypotenuse of the triangle will be the length of the ladder. We will use the formula as below:
$\sin \theta = \dfrac{{{\text{Side opposite to the angle}}}}{{{\text{Hypotaneous}}}}$and $\tan \theta = \dfrac{{{\text{Side opposite to the angle}}}}{{{\text{Side adjacent to the angle}}}}$.

Complete step-by-step answer:
Step 1: First of all, we will draw the triangle where ${\text{AD}}$ is the pole which meets the ladder at a point ${\text{B}}$ to the ground with an angle of $60^\circ$ at the point
${\text{C}}$:

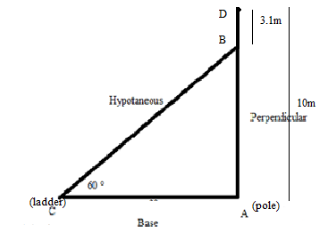
Step 2: Now, as the person needs to reach a point
${\text{3}}{\text{.1m}}$ below the top of the pole to undertake the repair work we will calculate the height ${\text{AB}}$:
Height of the pole ${\text{AD}} = 10{\text{m}}$ and ${\text{BD}} = 3.1{\text{m}}$, by substituting these values in ${\text{AB}} = {\text{AD}} - {\text{BD}}$ we get:
$\Rightarrow {\text{AB}} = 10 - 3.1$
By subtracting on the RHS side we get the value of ${\text{AB}}$:

$\Rightarrow {\text{AB}} = 6.9$
Step 2: Now, we need to find the length of the ladder ${\text{BC}}$ and the distance from the foot of the ladder to the foot of the pole i.e. ${\text{AC}}$ .
Since the pole is vertical to the ground so, $\Delta {\text{BAC}}$ will be a right angle triangle, where, ${\text{AB}} = {\text{Perpendicular = 6}}{\text{.9}}$,
${\text{AC}} = {\text{Base}}$ and ${\text{BC}} = {\text{Hypotenuse}}$.
Step 3: Now by using the formula for $\sin \theta = \dfrac{{{\text{Side opposite to the angle}}}}{{{\text{Hypotenuse}}}}$ in right angle triangle $\Delta {\text{BAC}}$ :
$\sin \theta = \dfrac{{{\text{Side opposite to the angle}}}}{{{\text{Hypotenuse}}}} = \dfrac{{{\text{AB}}}}{{{\text{BC}}}}$…………….. (1)
The value of the angle
$\angle {\text{ACB = 6}}{{\text{0}}^o}$also ${\text{AB = 6}}{\text{.9}}$ so, by putting these values in the above expression (1):
$\Rightarrow \sin {60^o} = \dfrac{{6.9}}{{{\text{BC}}}}$
Step 4: We know that the value of $\sin {60^o} = \dfrac{{\sqrt 3 }}{2}$, substituting this value in $\sin {60^o} = \dfrac{{\sqrt 3 }}{2}$ the above equation $\sin {60^o} = \dfrac{{6.9}}{{{\text{BC}}}}$, we get:
$\Rightarrow \dfrac{{\sqrt 3 }}{2} = \dfrac{{6.9}}{{{\text{BC}}}}$ ……….. (2)
By taking ${\text{BC}}$ in the LHS side and $2$ RHS side in the above equation (2), we get:
$\Rightarrow \sqrt 3 {\text{BC = 6}}{\text{.9}} \times {\text{2}}$
By dividing the RHS side by $\sqrt 3$ in the above equation $\sqrt 3 {\text{BC = 6}}{\text{.9}} \times {\text{2}}$, we get:
$\Rightarrow {\text{BC = }}\dfrac{{{\text{6}}{\text{.9}} \times {\text{2}}}}{{\sqrt 3 }}$
In the RHS side, by multiplying the numerator first and then dividing the result by denominator in the above equation ${\text{BC = }}\dfrac{{{\text{6}}{\text{.9}} \times {\text{2}}}}{{\sqrt 3 }}$ , we get:
$\Rightarrow {\text{BC = }}7.96{\text{m}}$
So, the length of the ladder is ${\text{BC = }}7.96{\text{m}}$.
Step 5: Now, for finding the distance from the foot of the pole to the foot of the ladder, we will use the formula
$\tan \theta = \dfrac{{{\text{Side opposite to the angle}}}}{{{\text{Side adjacent to the angle}}}}$in $\Delta {\text{BAC}}$.
The side opposite to the angle $\angle {\text{ACB}}$ is ${\text{AB}}$ and the side adjacent to the angle $\angle {\text{ACB}}$ is ${\text{AC}}$. By substituting these values in the formula $\tan \theta = \dfrac{{{\text{Side opposite to the angle}}}}{{{\text{Side adjacent to the angle}}}}$ we get:
$\Rightarrow \tan \theta = \dfrac{{{\text{AB}}}}{{{\text{AC}}}}$ …………. (3)
The value of the angle $\angle {\text{ACB = 6}}{{\text{0}}^o}$also ${\text{AB = 6}}{\text{.9}}$ so, by putting these values in the above expression (3):
$\Rightarrow \tan {60^o} = \dfrac{{6.9}}{{{\text{AC}}}}$
We know that the value of $\tan {60^o} = \sqrt 3$, substituting this value in $\tan {60^o} = \sqrt 3$ in the above equation $\tan {60^o} = \dfrac{{6.9}}{{{\text{AC}}}}$, we get:
$\Rightarrow \sqrt 3 = \dfrac{{6.9}}{{{\text{AC}}}}$ ……….. (4)
By taking
${\text{AC}}$in the LHS side in the above equation (4), we get:
$\Rightarrow \sqrt 3 {\text{AC = 6}}{\text{.9}}$
By dividing the RHS side by $\sqrt 3$ in the above equation $\sqrt 3 {\text{AC = 6}}{\text{.9}}$, we get:
$\Rightarrow {\text{AC = }}\dfrac{{{\text{6}}{\text{.9}}}}{{\sqrt 3 }}$
In the RHS side, by dividing the numerator with the denominator in the above equation ${\text{AC = }}\dfrac{{{\text{6}}{\text{.9}}}}{{\sqrt 3 }}$ , we get:
$\Rightarrow {\text{AC = 3}}{\text{.98m}}$

So, the distance from the foot of the ladder and pole is ${\text{3}}{\text{.98m}}$.

Note: Students should not confuse between sine and tan value for $60^\circ$, below are the values for sine, cosine, and tan which students should remember:

| ${0^0}$| ${30^0}$| ${45^0}$| ${60^0}$| ${90^0}$
---|---|---|---|---|---
sin| $0$| $\dfrac{1}{2}$| $\dfrac{{\sqrt 2 }}{2}$| $\dfrac{{\sqrt 3 }}{2}$| $1$
cos| $1$| $\dfrac{{\sqrt 3 }}{2}$| $\dfrac{{\sqrt 2 }}{2}$| $\dfrac{1}{2}$| $0$
tan| $0$| $\dfrac{{\sqrt 3 }}{3}$| $1$| $\sqrt 3$| Undefined

So, be careful in that part. Also, understand the question properly at the time of making the diagram.