Question

An electric pole is 10 meters high. A steel wire tied to the top of the pole is affixed at a point on the ground to keep the pole upright. If the wire makes an angle ${{45}^{\circ }}$ with the horizontal through the foot of the pole, find the length of the wire.

Answer 1

Hint:We will draw the diagram with AB as the electric pole and AC as the steel wire. Since, we need to find the length of the wire so, we will apply the formula of trigonometric ratios which is given by $\sin \left( \theta \right)=\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$. Here, the value of $\theta ={{45}^{\circ }}$.

Complete step-by-step answer:
The diagram for the question is given below.

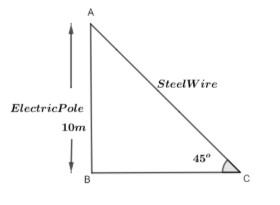
In the diagram we can clearly see that the steel wire that is tied to the ground is denoted as AC. The height of the electric pole is denoted as AB. BC is the distance between the bottom of the electric pole to the bottom of the steel wire which is tied to the ground. We are here asked to find the length of the steel wire. For this we will use the formula of trigonometric ratios which is given by $\sin \left( \theta \right)=\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$. Here, the value of $\theta ={{45}^{\circ }}$. Therefore, we have $\sin \left( {{45}^{\circ }} \right)=\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$. Since, the perpendicular is AB whose length is given as 10 meters which is the height of the electric pole and the hypotenuse is given by the length AC. Thus, we have
$\begin{aligned} & \sin \left( {{45}^{\circ }} \right)=\dfrac{\text{Perpendicular}}{\text{Hypotenuse}} \\\ & \Rightarrow \sin \left( {{45}^{\circ }} \right)=\dfrac{AB}{AC} \\\ \end{aligned}$
As the length AB is 10 meters. Thus we get
$\begin{aligned} & \sin \left( {{45}^{\circ }} \right)=\dfrac{AB}{AC} \\\ & \Rightarrow \sin \left( {{45}^{\circ }} \right)=\dfrac{10}{AC} \\\ \end{aligned}$
As we know that the value of $\sin \left( {{45}^{\circ }} \right)=\dfrac{1}{\sqrt{2}}$ therefore, we have
$\begin{aligned} & \sin \left( {{45}^{\circ }} \right)=\dfrac{10}{AC} \\\ & \Rightarrow \dfrac{1}{\sqrt{2}}=\dfrac{10}{AC} \\\ & \Rightarrow \dfrac{10}{AC}=\dfrac{1}{\sqrt{2}} \\\ & \Rightarrow AC=10\times \sqrt{2} \\\ \end{aligned}$
Since, the value of $\sqrt{2}=1.41$ therefore we have $AC=10\times \sqrt{2}$ as $AC=10\times 1.41$ or, $AC=14.1$.
Hence, the length of the steel wire is 14.1 meters.

Note: One should always check the units in order to write a completely correct answer. If we had taken $\sqrt{2}=1.4142135624$ then we would have got $AC=14.1421356237$ which is approximately equal to $AC=14.1$. So, taking $\sqrt{2}=1.41$ here is also correct. Alternate method to solve the question is using the formula $\text{cosec}\left( \theta \right)=\dfrac{\text{Hypotenuse}}{\text{Perpendicular}}$. Here, the value of $\theta ={{45}^{\circ }}$. Therefore, we have $\text{cosec}\left( {{45}^{\circ }} \right)=\dfrac{\text{Hypotenuse}}{\text{Perpendicular}}$. Since, the perpendicular is AB whose length is given as 10 meters which is the height of the electric pole and the hypotenuse is given by the length AC. Thus, we have
$\begin{aligned} & \text{cosec}\left( {{45}^{\circ }} \right)=\dfrac{\text{Hypotenuse}}{\text{Perpendicular}} \\\ & \Rightarrow \text{cosec}\left( {{45}^{\circ }} \right)=\dfrac{AC}{AB} \\\ \end{aligned}$
As the length AB is 10 meters. Thus we get
$\begin{aligned} & \text{cosec}\left( {{45}^{\circ }} \right)=\dfrac{AC}{AB} \\\ & \Rightarrow \text{cosec}\left( {{45}^{\circ }} \right)=\dfrac{AC}{10} \\\ \end{aligned}$
As we know that the value of $\text{cosec}\left( {{45}^{\circ }} \right)=\sqrt{2}$ therefore, we have
$\begin{aligned} & \text{cosec}\left( {{45}^{\circ }} \right)=\dfrac{AC}{10} \\\ & \Rightarrow \sqrt{2}=\dfrac{10}{AC} \\\ & \Rightarrow \dfrac{10}{AC}=\sqrt{2} \\\ & \Rightarrow AC=10\times \sqrt{2} \\\ \end{aligned}$
Since, the value of $\sqrt{2}=1.41$ therefore we have $AC=10\times \sqrt{2}$ as $AC=10\times 1.41$ or, $AC=14.1$.
Hence, the length of the steel wire is 14.1 meters.
We can also use other trigonometric ratios i.e $\tan$ ,$\cos$ ,$\cot$ to solve this question we get one unknown value and consider it as one equation and use another trigonometric ratio equate it to the first equation,by simplifying and using standard angles we get the same answer.