Question

An electric motor operates on a 50 volt supply and draws a current of 12 A. If the efficiency of the motor is 30%, find the resistance of the windings of the motor.
A) $3.4\Omega$
B) $2.1\Omega$
C) $3.9\Omega$
D) $2.9\Omega$

Answer 1

For a motor working with an efficiency of 30%, the percentage of power loss must be 70%. The resistance of the windings contributes to this loss in power.

Formula Used:

1. Power drawn from the circuit is given by, ${P_{drawn}} = VI$ where $V$ is the supply voltage and $I$ is the current drawn from the circuit.
2. Power lost in the circuit is given by, ${P_{loss}} = {I^2}R$ where $I$ is the current drawn from the circuit and $R$ is the resistance of the circuit.

Complete step by step answer:
Step 1: Sketch a circuit showing the flow of current in the circuit.

Circuit representing the resistance of windings of the motor

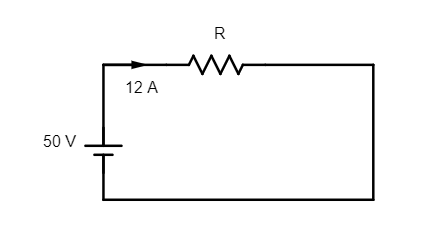
Step 2: List the key points mentioned in the question.
The supply voltage of the motor is $V = 50{\text{V}}$ and the current drawn from the circuit is $I = 12{\text{A}}$ .
The efficiency of the motor is 30 % i.e., $\eta = \dfrac{{30}}{{100}} = 0.3$
Step 3: Calculate the power drawn from the circuit.
Power drawn from the circuit is given by, ${P_{drawn}} = VI$ ---------- (1) where $V$ is the supply voltage and $I$ is the current drawn from the circuit.
Substituting for $V = 50{\text{V}}$ and $I = 12{\text{A}}$ in equation (1) we get ${P_{drawn}} = 50 \times 12 = 600{\text{W}}$
So, the power drawn will be ${P_{drawn}} = 600{\text{W}}$ .
Step 4: Find the resistance of the windings by calculating the loss of power in the circuit.
As the efficiency of the motor is only 30 %, the remaining 70 % constitutes the loss in power.
So the loss in power will be ${P_{loss}} = \dfrac{{70}}{{100}} \times {P_{drawn}}$
Substituting the value for ${P_{drawn}} = 600{\text{W}}$ in the above equation, we get ${P_{loss}} = \dfrac{{70}}{{100}} \times 600 = 420{\text{W}}$
This power is lost across the resistance of the windings of the motor.
Power lost in the circuit is given by, ${P_{loss}} = {I^2}R$ --------- (2) where $I$ is the current drawn from the circuit and $R$ is the resistance of the circuit.
Substituting the value for ${P_{loss}} = 420{\text{W}}$ and $I = 12{\text{A}}$ in equation (2) we get, $420 = {12^2}R$
Solving for $R$ we get, $R = \dfrac{{420}}{{{{12}^2}}} = 2.9\Omega$
$\therefore$ the resistance of the windings of the electric motor is $R = 2.9\Omega$ .
Thus, the correct option is D.

Note: The power loss in a circuit refers to the amount of power that was drawn from the circuit but does not contribute to the output power of the circuit. So power loss will be the difference in the power drawn and the output power of the motor i.e., ${P_{loss}} = {P_{drawn}} - {P_{out}}$
Since the efficiency of the motor is $\eta = 0.3$, the output power will be ${P_{out}} = 600 \times 0.3 = 180{\text{W}}$
Then the power loss will be ${P_{loss}} = 600 - 180 = 420{\text{W}}$
This loss in power is then generated as heat in the circuit.