Question

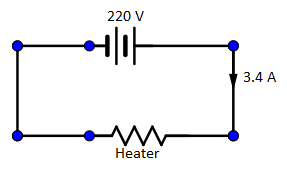
An electric heater draws a current of $3.4A$ from the $220V$ supply line. What current will it draw when connected to the $110V$ supply line?
(A) $6.8A$
(B) $1.7A$
(C) $13.6A$
(D) $27.2A$

Answer 1

In order to find the current during the supply line voltage, we can use the Ohm’s law which deals with the current flow. In order to find the current first we have to find the resistance that is created by current flowing through the water heater first hand.

Formula used:
By using the formula derived from Ohm’s law;
$V = IR$
Where $V$ denotes the voltage, $I$ denotes the current, $R$ denotes the resistance.

Complete step by step solution:
Given data:
Current drawn by the electric heater, $I = 3.4A$,
Voltage used by electric heater, $V = 220V$,
Another voltage, $V = 110V$

According to Ohm’s law the formula is;
$V = IR$
Since we have to find the resistance $R$ ;
By rearranging the formula, we get;
$R = \dfrac{V}{I}$
Substitute the values of voltage $V$ , the current $I$;
When the voltage $V = 220V$ is;
$\Rightarrow R = \dfrac{{220V}}{{3.4A}}$
On simplifying the above equation, we get;
$\Rightarrow R = 64.7 \Omega$
Therefore, the resistance on the electric heater is $R = 64.7 \Omega$ when the voltage is $V = 220V$

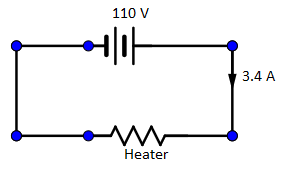
When the voltage on the electric heater is $V = 110V$ ;
$V = IR$
since we need current when $V = 110V$
by rearranging the formula;
$I = \dfrac{V}{R}$
Substitute the values of $V = 110V$ and $R = 64.7 \Omega$ ;
$\Rightarrow I = \dfrac{{110V}}{{64.7 \Omega }}$
On simplification we get;
$\Rightarrow I = 1.7A$
Therefore, the current drawn by the electric heater when it is connected to the supply line of $110V$ is $I = 1.7A$.

Hence, the option (B), $I = 1.7A$ is the correct answer.

Note: We have to keep in mind that the voltage of the supply line here varies, so we have to substitute the correct voltage value for every stage of the problem. At the end each solution we definitely have to add the appropriate S.I. unit to it. The voltage is directly proportional to the current and resistance.