Question

An electric dipole of dipole moment $\vec p$ is placed in a uniform $\vec E$ Obtain the expression for the torque $\vec \tau$ experienced by the dipole. Identify two pairs of perpendicular vectors in expression.

Answer 1

In order to solve this question we need to understand Electric field and electric dipole. Electric field is defined as a line of action of forces around a charge on which when another charge places it experiences force either towards or opposite it. Electric dipole is defined as a system of two equal and opposite charges kept at some distance and torque is defined as rotating force, it is mathematically defined as a product of a pair of equal magnitude of opposite forces and the perpendicular distance from the axis of rotation.

Complete step by step answer:
Consider an electric dipole (system of $+ q\& \- q$ placed at distance $l$ ) placed in a uniform electric field such that it makes an angle $\theta$ with direction of uniform electric field.

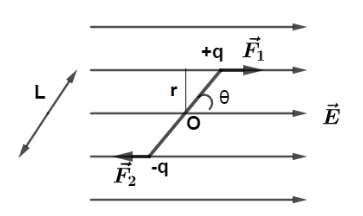
So Force on $+ q$ charge due to $\vec E$ field is given by, ${\vec F_1} = q\vec E$ and its direction is along the fiel. The force on $- q$ charge due to $\vec E$ field is given by, ${\vec F_2} = - q\vec E$ and its direction is opposite to the field. So the two forces are equal in magnitude, which is ${F_1} = {F_2}$.

And exactly opposite to each other so net force on the system is $0$. So, the body could not translate, rather it would rotate as a couple of forces. Let $r$ be the perpendicular distance from the axis of rotation to the line of action of force so torque by both the forces would try to align the dipole in the direction of the field by rotating it anticlockwise.Torque to force ${\vec F_1}$ is given by,
${\vec \tau _1} = r{\vec F_1}$
Since, from geometry,
$\sin \theta = \dfrac{r}{{\dfrac{l}{2}}}$
$\Rightarrow r = \dfrac{l}{2}\sin \theta$

Putting values we get torque magnitude as, ${\tau _1} = qE\sin \theta (\dfrac{l}{2})$
Similarly Torque due to force ${\vec F_2}$ is given by, ${\vec \tau _2} = r{\vec F_2}$
Putting values we get torque magnitude as, ${\tau _2} = qE\sin \theta (\dfrac{l}{2})$
Both torque are in same direction, hence they try to rotate the dipole in anticlockwise sense,
So Net torque is $\tau = {\tau _1} + {\tau _2}$
Putting values we get, $\tau = qE\sin \theta (\dfrac{l}{2}) + qE\sin \theta (\dfrac{l}{2})$
$\tau = qlE\sin \theta$
Since dipole is given by, $p = ql$
So torque becomes, $\tau = pE\sin \theta$
$\therefore \vec \tau = \vec p \times \vec E$
And two perpendicular forces are, ${\vec F_1} = q\vec E$ and ${\vec F_2} = - q\vec E$.

Note: It should be remembered that here the net electric field at a large distance varies as per dipole not due to monopole or Quadrupole because monopole is zero or net charge is zero. And we know from multipole expansion that when a monopole is zero then the electric field varies as dipole. Also Torque tries to align the electric dipole in the direction of the field so as to minimize potential energy.