Question

An electric dipole is kept on the axis of a uniformly charged ring at distance $\sqrt 2 R$ from the centre of the ring. The direction of the dipole moment is along the axis, the dipole moment is P, charge of the ring Q and radius of the ring is R. The force on the dipole is:
A. $\dfrac{{4kpQ}}{{3\sqrt 3 {R^S}}}$
B. $\dfrac{{kpQ}}{{3\sqrt 3 R}}$
C. $\dfrac{{2kpQ}}{{3\sqrt 3 {R^S}}}$
D. Zero

Answer 1

We know that the electric field is the region produced by an electric charge around it whose influence is observed when another charge is brought in that region where the field exists. So, to find the force on the dipole we first find the electric field then apply the formula.

Formula used:
$E = \dfrac{{k{Q_1}{Q_2}}}{{{R^2}}}$
$F = P\dfrac{{dE}}{{dx}}$

Complete step-by-step answer:
The electric field due to ring along its axis can be written as, $E(x) = \dfrac{{kQx}}{{{{({x^2} + {R^2})}^{3/2}}}}$; where $x$ is the separation between the centre of the ring to the observation point, Q is the charge on the ring and R is the radius of the ring as shown below:

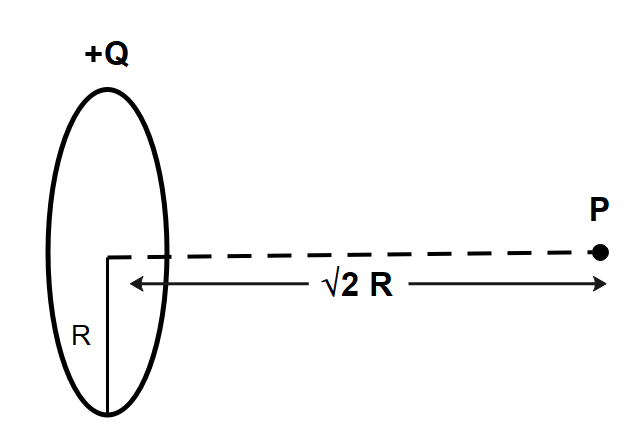
We know that force on the dipole is given by, $F = P\dfrac{{dE}}{{dx}}$
Now, we will differentiate the electric field with respect to $x$ ,
$\dfrac{{dE}}{{dx}} = kQ\left[ {\dfrac{{({x^2} + {R^2}) - \dfrac{3}{2}{{({x^2} + {R^2})}^{1/2}}2x.x}}{{{{({x^2} + {R^2})}^3}}}} \right]$
$= kQ\sqrt {({x^2} + {R^2})} \left[ {\dfrac{{{x^2} + {R^2} - 3{x^2}}}{{{{({x^2} + {R^2})}^3}}}} \right]$
$= kQ\sqrt {({x^2} + {R^2})} \left[ {\dfrac{{{R^2} - 2{x^2}}}{{{{({x^2} + {R^2})}^3}}}} \right]$
Now, at $x = \sqrt 2 R$ we will find the value of $\dfrac{{dE}}{{dx}}$
\dfrac{{dE}}{{dx}} = kQ\sqrt {(2{R^2} + {R^2})} \left[ {\dfrac{{{R^2} - 2{{(\sqrt 2 R)}^2}}}{{{{\left\\{ {{{(\sqrt 2 R)}^2} + {R^2}} \right\\}}^3}}}} \right] $= kQ\sqrt 3 {R^2}\left[ {\dfrac{{{R^2} - 4{R^2}}}{{{{(2{R^2} + {R^2})}^3}}}} \right]$
$\Rightarrow \dfrac{{dE}}{{dx}} = kQ\sqrt 3 {R^2}\left[ {\dfrac{{ - 3{R^2}}}{{27{R^5}}}} \right]$ $= - kQ\dfrac{{\sqrt 3 }}{{9R}} = - kQ\dfrac{1}{{3\sqrt 3 R}}$
So, the force on the dipole will be,
$F = P\dfrac{{dE}}{{dx}}$
Here, we are only considering the magnitude of the force so negative signs can be neglected.
$\Rightarrow F = \dfrac{{kPQ}}{{3\sqrt 3 R}}$

So, the correct answer is “Option B”.

Additional Information: The direction of the electric field is directed away from the positive source of charges. While it is directed towards the negative source of charges.
In electromagnetism, there are two types of dipoles. An electric dipole is defined as the couple of opposite charges $q$ and $- q$ separated by a distance $d$. The midpoint of the two charges is known as the centre of the dipole. It is denoted by the symbol $\overrightarrow p$. It is a vector quantity.

Note: The net force acting on a dipole placed in a uniform electric field is equal and opposite, so the net force is zero.