Question

An electric dipole is formed by two equal and opposite charges q with separation d. The charges have the same mass m. It is kept in a uniform electric field E. If it is slightly rotated from its equilibrium orientation, then its angular frequency is:
A. $\sqrt{\dfrac{qE}{2md}}$
B. $\sqrt{\dfrac{qE}{md}}$
C. $\sqrt{\dfrac{2qE}{md}}$
D. $\sqrt{\dfrac{qE}{md}}$

Answer 1

In this question we have been asked to calculate the angular frequency of the electric dipole when it is rotated by a small angle from its equilibrium position in the given electric field. To solve this question, we shall first calculate the torque on the system. We know that torque is also given as a product of angular acceleration and moment of inertia. Therefore, we shall calculate the moment of inertia and then equate the two calculated torque. In doing so, we shall calculate the angular frequency using the angular acceleration.

Formula used:
$\tau =PE\sin \theta$
$\tau =I\alpha$
$\alpha ={{\omega }^{2}}\theta$

Complete step by step answer:
The electric dipole is formed by two equal and opposite charges q with separation d in uniform magnetic field as shown in the figure below.

It is said that initially the dipole was in equilibrium but later it was rotated with a small angle say $\theta$ as shown in the figure below.

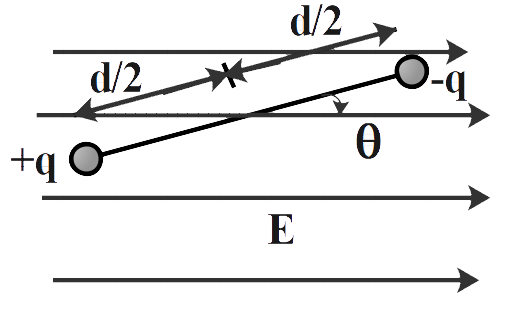
Now, we know torque on electric dipole system in uniform electric field is given by,
$\tau =PE\sin \theta$
We know that electric dipole is given as,
$P=qd$
Therefore, we can say that,
$\tau =qdE\sin \theta$
Now it is given that $\theta$ is very small
Therefore, we can assume $\sin \theta =\theta$
Therefore, we get
$\tau =qdE\theta$ ………….. (1)
Now, we also know that,
$\tau =I\alpha$ …………… (2)
Therefore, from (1) and (2) we get,
$I\alpha =qdE\theta$
Solving for $\alpha$
$\alpha =\dfrac{qdE\theta }{I}$ ……………………. (3)
We also know that,
$\alpha ={{\omega }^{2}}\theta$ ……………….. (4)
From (3) and (4)
We get,
${{\omega }^{2}}=\dfrac{qdE}{I}$ …………………. (5)
Now, solving for I
We know that moment of inertia is given by,
$I={{m}_{1}}r_{1}^{2}+{{m}_{2}}r_{2}^{2}$
Now the distance of the dipole from the centre is d/2 as shown in the figure
Therefore,
$I=m{{\left( \dfrac{d}{2} \right)}^{2}}+m{{\left( \dfrac{d}{2} \right)}^{2}}$
On solving we get,
$I=\dfrac{m{{d}^{2}}}{2}$ …………………. (6)
Substituting the value of I in equation (5)
We get,
${{\omega }^{2}}=\dfrac{qdE}{\dfrac{m{{d}^{2}}}{2}}$
On solving we get,
$\omega =\sqrt{\dfrac{2qE}{md}}$
Therefore, the correct answer is option C.

Note: When a pair of equal and opposite charged particles is separated by some distance, the system is known as electric dipole. The measure of rotation of an object about a point is called torque. The net force on the dipole is zero, therefore, when the dipole is rotated at an angle with the electric field torque is applied on the system at the point equidistant from the charges. This happens as the dipole tends to align with the electric field.