Question

An electric current I enters and leaves a uniform circular wire of radius a through diametrically opposite points. A charged particle q moving along the axis of the circular wire passes through its center at speed v. The magnetic force acting on the particle when it passes through the center has a magnitude
$\left( A \right)qv\dfrac{{\mu 0i}}{{2a}}$
$\left( B \right)qv\dfrac{{\mu 0i}}{{2\pi a}}$
$\left( C \right)qv\dfrac{{\mu 0i}}{a}$
$\left( D \right)zero$

Answer 1

First we will make a diagram and show the direction of current flowing through the circular wire. Analyzing the diagram we can see that the current gets divided diametrically on the circular wire now using the given values we can find the magnetic force acting on the particle.

Complete step by step solution:
As per the given problem we know that an electric current I enters and leaves a uniform circular wire of radius a through diametrically opposite points. A charged particle q moving along the axis of the circular wire passes through its center at speed v.
We need to calculate the magnetic force acting on the particle when it passes through the center.
Now according to the given statement

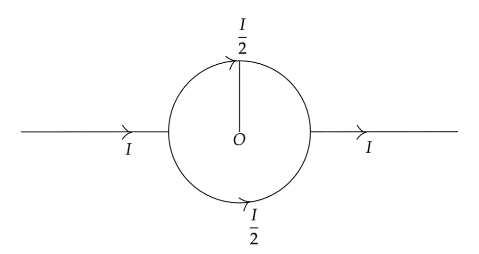
Now from the above diagram,
The direction of forces are opposite to each other due to the direction of current in the loop. Now using Fleming’s right hand rule we can see that force acting on the center of circular wire is equal in magnitude but opposite in direction.
We know,
Force is acting downward in the upper segment of the circular wire while force is upward due to the lower segment.
We know Magnetic force,
$F = vqB$
Where,
Velocity of a charged particle is v.
Charge is q.
And the magnetic field due to this moving charge is B.
We know, $B = \dfrac{{\mu 0I}}{{2\pi d}}$
Now putting this value in the magnetic force formula we will get,
$F = vq\dfrac{{\mu 0I}}{{2\pi a}}$
Here the radius of the circular wire is a.
As we can see from the figure the current get divided equally in two segment diametrically hence the net force acting on the center is equals to,
$F_{net} = F_1 + F_2$
Both $F_1\,and\,F_2$ are opposite in direction to each other but magnetic are same hence we can write net force as,
$F_{net} = vq\dfrac{{\mu 0\dfrac{I}{2}}}{{2\pi a}} - vq\dfrac{{\mu 0\dfrac{I}{2}}}{{2\pi a}}$
Therefore the correct option is $\left( D \right)$ .

Note:
Remember that in Fleming’s right hand rules if we hold our right hand the forefinger represents the direction of magnetic field, middle finger represents the direction of current and the thumb represents the direction of force and all the three figures are perpendicular to each other.