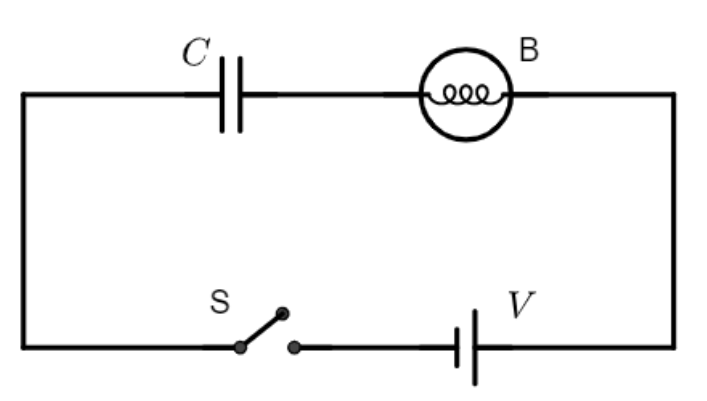
Question

An electric bulb, a capacitor, a battery and a switch are all in series in a circuit. How does the intensity of light vary when the switch is turned on?

A. Continues to increase gradually
B. Gradually increases for some time and then becomes steady
C. Sharply rises initially and then gradually decreases
D.Gradually increases for some time and then gradually decreases.

Answer 1

We can treat this circuit as an RC circuit, with the bulb as the resistance and the capacitor as the capacitance. We know that when the switch is closed, the capacitor begins charging from the supply voltage via the bulb resistance. Initially, the bulb receives all of the supply voltage and then it starts losing out on the incident voltage as the capacitor begins charging.
Begin by first finding out the voltage drop across the capacitor at any instant of time. Then subtract this from the supply voltage to obtain the voltage across the bulb and find its power. From the resulting expression, you should be able to estimate the kind of plot you would get for power against time, following which you can pick out the appropriate option.

Formula used:
Voltage across a capacitor: $V_C = V(1-e^{-t/RC})$

Complete step by step answer:
From the circuit we see that there will be voltage drops across the capacitor and the bulb. The bulb is equivalent to a resistor. Now, when a resistor is connected in series with a capacitor forming an RC circuit, the capacitor will charge up gradually through the resistor until the voltage across it reaches the supply voltage V. Thus, the capacitor takes some time to be fully charged which we call as the transient response time. For a given value of resistance R and capacitance C, the transient time remains constant and is called as the RC time constant $\tau = R \times C$.

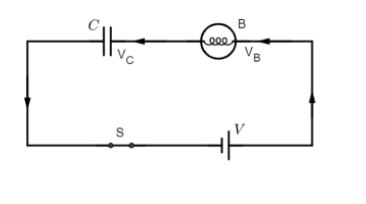
Thus, for a supply voltage V, the instantaneous voltage across the capacitor is given as
$V_C = V(1-e^{-t/RC}) \Rightarrow V_C = V(1-e^{-t/\tau})$
We know that, for a series circuit, the current across all circuit components remains the same but the voltage drops vary.
Therefore, the voltage drop across the bulb B with resistance R can be given as
$V_B = V – V_C = V - V(1-e^{-t/\tau})$
$\Rightarrow V_B = Ve^{-t/\tau}$
Now, the intensity of the bulb is given by its power
$P_B = \dfrac{V_B^2}{R} = \dfrac{ V^2 e^{-2t/\tau}}{R} \Rightarrow P_B \propto e^{-2t/\tau}$
Thus, when we plot the intensity of light versus time, we get an exponentially decreasing curve, with an initial sharp rise at t=0.

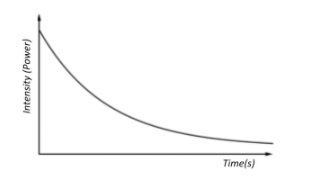
Thus, the correct choice would be C. Sharply rises initially and then gradually decreases

Note:
Do not get confused between the transient period and the steady state period of a capacitor.
The transient period is the period during which the capacitor gets charged, starting from an uncharged state. This signifies a transition between two states, from uncharged to charged. The steady state period however, is the time after the transient period where the voltage across the capacitor attains a constant value that is consistent with the supply voltage. At steady state, the capacitor acts as an open circuit since it attains a voltage equivalent to the supply voltage and there is no potential difference between them because of which no charge or current flows between them.