Solveeit Logo
Login

Question

Question: An elasticized conducting band is around a spherical balloon (figure). Its plane passes through the ...

An elasticized conducting band is around a spherical balloon (figure). Its plane passes through the center of the balloon. A uniform magnetic field of magnitude 0.04 T is directed perpendicular to the plane of the band. Air is let out of the balloon at 100cm3/s100c{{m}^{3}}/s at an instant when the radius of the balloon is 10cm. The induced emf in the band is :

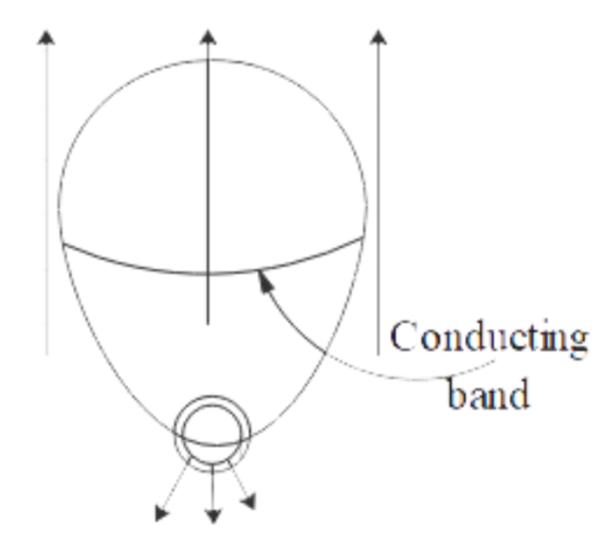
A. 15 μV\mu V
B. 25 μV\mu V
C. 10 μV\mu V
D. 20 μV\mu V

Explanation

Solution

In this question we are asked to find induced emf. So, it is clear that we will be using the formula for induced emf. We will also find the rate of change of radius as we need to substitute the value in the emf equation for the area. Also, the options are given in SI units, therefore we need to make the necessary conversion of the unit from centimeter to the meter.

Formula Used:
ε=−dϕdt\varepsilon =-\dfrac{d\phi }{dt}
ϕ=BAcos⁡θ\phi =BA\cos \theta
V=43πr3V=\dfrac{4}{3}\pi {{r}^{3}}

Complete step-by-step solution:
Let us first convert the units into Si units.
Therefore, r = radius of balloon = 10×10−210\times {{10}^{-2}} m. rate of change of volume of spherical balloon = 100×10−6100\times {{10}^{-6}} m.
We know, the formula of induced emf is given by,
ε=−dϕdt\varepsilon =-\dfrac{d\phi }{dt} ………………………….. (1)
We also, know the formula for magnetic flux,
ϕ=BAcos⁡θ\phi =BA\cos \theta …………………………. (2)
Let us now find the rate of change of radius as it is given that the conduction band is in the center plane of the balloon. This means that the rate of change of flux will depend on the rate of change of radius.
We know,
V=43πr3V=\dfrac{4}{3}\pi {{r}^{3}} ………………………… (3)
Differentiating both sides with respect to t
We get,
dVdt=43π×3r2drdt\dfrac{dV}{dt}=\dfrac{4}{3}\pi \times 3{{r}^{2}}\dfrac{dr}{dt}
dVdt=4πr2drdt\dfrac{dV}{dt}=4\pi {{r}^{2}}\dfrac{dr}{dt}
∴drdt=14πr2dVdt\therefore \dfrac{dr}{dt}=\dfrac{1}{4\pi {{r}^{2}}}\dfrac{dV}{dt} ……………………….. (4)
Now, for change in magnetic flux.
Since, the area vector and magnetic field vector are in same direction
We know that,
θ=1,A=πr2\theta =1, A=\pi {{r}^{2}}
After substituting these values in (2)
We get,
∴ϕ=Bπr2\therefore \phi =B\pi {{r}^{2}}
Again differentiating with respect to t
dϕdt=π×B×2rdrdt\dfrac{d\phi }{dt}=\pi \times B\times 2r\dfrac{dr}{dt} ……………………………… (5)
Substituting (5) in equation (1)
We get,
ε=−dϕdt=−π×B×2rdrdt\varepsilon =-\dfrac{d\phi }{dt}=-\pi \times B\times 2r\dfrac{dr}{dt}
After substituting the value from equation (4) in above equation
We get,
ε=−B×2πr×14πr2(−dVdt)\varepsilon =-B\times 2\pi r\times \dfrac{1}{4\pi {{r}^{2}}}(-\dfrac{dV}{dt})
In the above equation we took −dVdt-\dfrac{dV}{dt} because the area of the spherical balloon is decreasing.
Therefore,
ε=−B×12r×(−dVdt)\varepsilon =-B\times \dfrac{1}{2r}\times (-\dfrac{dV}{dt})
Now let us substitute the given values
ε=−0.042×10×10−2×(−100×10−6)\varepsilon =-\dfrac{0.04}{2\times 10\times {{10}^{-2}}}\times \left( -100\times {{10}^{-6}} \right)
ε=20×10−6V\varepsilon =20\times {{10}^{-6}}V
This can also be written as,
ε=20μV\varepsilon =20\mu V
Therefore, the correct answer is option D.

Additional Information: In physics and maths the term 10−6{{10}^{-6}} is taken as μ\mu , similarly as 10−9{{10}^{-9}} is called nano.

Note: If the magnetic flux through a coil is changed, the voltage will be produced. This voltage is known as the induced emf. In this question, the emf is produced due to the reducing size of the band, hence due to the change in volume of the spherical balloon with time.