Question
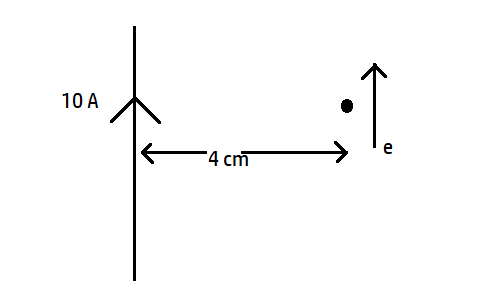
Question: An e is moving parallel to a long current carrying wire with a velocity \[v={{10}^{5}}m/s\]as shown,...
An e is moving parallel to a long current carrying wire with a velocity v=105m/sas shown, force on electron is?
A- 0.4×10−18N
B- 0.8×10−18N
C- 0.8×10−16N
D- 1.6×10−18N
Solution
We are given an electron placed at some distance from a current carrying wire. We know a current carrying wire generates a magnetic field. And we know moving charged particles experience a force in an external magnetic field.
Step by step answer:
Magnitude of charge= 1.6×10−19C
The magnetic force on a charged particle placed in a magnetic field is given by F=q(v×B)
But we need to first calculate the value of the field due to a long current carrying wire. We know the magnetic field due to a long current carrying wire at a distance from it by B=4π×rμ0×2I.
Here r is the perpendicular distance from the wire and I is the current in the wire
Here r = 4 cm = 0.04 m and I= 10 A
B=4π×rμ0×2I=0.0410−7×2×10=5×10−5T
The direction of the field is into the plane of paper using the right hand thumb rule.
Now force,
The angle between the velocity and the field is 90∘, thus, F=qvB
F=1.6×10−19×105×5×10−5 ∴F=0.8×10−18NThus, the correct option is (B).
Note: Right-hand rule states that, if the thumb of the right hand is in the direction of the current flow then, the curl fingers show the direction of the magnetic field. We need to remember that the magnetic field is a vector quantity and we have to use right-hand thumb rules carefully while determining the direction of the field.
