Question
Question: An automobile vehicle has a mass of \(1500\,Kg\). What must be the force between the vehicle and roa...
An automobile vehicle has a mass of 1500Kg. What must be the force between the vehicle and road if the vehicle is to be stopped with a negative acceleration of 1.7ms−2 ?.
Solution
Hint
Use the formula given below and substitute the values of the mass and the acceleration of the vehicle in that formula. The answer obtained shows the force acting between the vehicle and the road that must help the vehicle to stop its movement.
The Newton’s second law of motion is
⇒F=ma
Where F is the force acting on the object, m is the mass of the object and the a is the acceleration acting on the object.
Complete step by step answer
The given data from the question is
The mass of the vehicle, m=1500Kg
The acceleration acts on the vehicle, a=−1.7ms−2 (since the acceleration makes the vehicle to stop)
The acceleration of the vehicle makes it stop by the application of the frictional force. Hence the frictional force between the road and the vehicle is calculated by using Newton's second law.
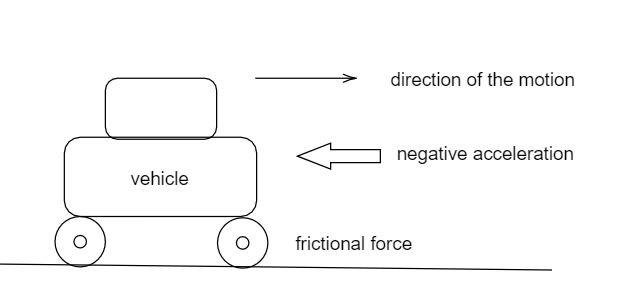
By using the formula,
⇒F=ma
Substituting the value of the mass and the acceleration of the vehicle in the above formula,
⇒F=1500×−1.7
By performing multiplication,
⇒F=−2550Kgms−2
We know that 1N=1Kgms−2
⇒F=−2550N
Thus the frictional force between the road and the vehicle is 2550N(negative since this stops the movement of the vehicle).
Note
The negative acceleration implies that this acceleration is required by the vehicle to stop its movement. Here the acceleration changes negative and opposite as the velocity. This acceleration that retards the movement said as the deceleration.
