Question

An automobile engine propels a 1000 kg car (A) along a leveled road at a speed of 36 km/h. Find the power if the opposing frictional force is 100 N.
Now, suppose after travelling a distance of 200 m, this car collides with another stationary car (B) of the same mass and comes to rest. Let its engine also stop at the same time. Now car (B) starts moving on the same level road without getting its engine started. Find the speed of the car (B) just after the collision.

Answer 1

We are given two cars A and B. At first we need to find the power of the car A. For that we know the equation to find power; by substituting the known values in the equation we get the power. Later it is said that this car hits the car B and B moves forward while A comes to rest. This is a case of inelastic collision and we know that momentum is conserved in this type of collision. Hence using this we can find the solution.

Formula used:
Power, $P=F\times v$
Momentum conserved,
$\begin{aligned} & mv=\text{constant} \\\ & \Rightarrow {{\text{m}}_{1}}{{v}_{1}}={{m}_{2}}{{v}_{2}} \\\ \end{aligned}$

Complete answer:
In the question we have two cars A and B and it is said that the mass of the two cars are the same.
${{m}_{A}}={{m}_{B}}=1000kg$, were ${{m}_{A}}$ is the mass of car A and ${{m}_{B}}$ is the mass of car B.
We are given a situation when the car A is moving forward along a level road with a speed 36 km/h and the opposing frictional force is given as 100 N.

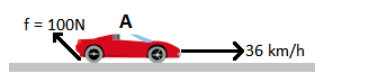
We have frictional force, $f=100N$
Velocity of the car A,
$\begin{aligned} & {{v}_{A}}=36km/h \\\ & \Rightarrow {{v}_{A}}=36\times \dfrac{5}{18}=10m/s \\\ \end{aligned}$
We need to find the power of the car.
We know that power is the product of force and velocity, i.e.
$P=F\times v$
Here the force is the frictional force, hence power of the car A
$\begin{aligned} & P=100\times 10 \\\ & P=1000W \\\ \end{aligned}$
The unit of power is Watt (W).
Now in the question, it is said that the car A collides with car B which is at rest after travelling a distance of 200 m.

After the collision the engine of car A stops working and car B starts to move on the road without getting its engine started.
In such a situation we know that the momentum is conserved, i.e. the momentum before collision will be the same as the momentum after collision.
Hence we have the formula,
${{m}_{A}}{{u}_{A}}+{{m}_{B}}{{u}_{B}}={{m}_{A}}{{v}_{A}}+{{m}_{B}}{{v}_{B}}$
In the above equation we know that ${{m}_{A}}\text{ and }{{m}_{B}}$ are the masses of the two cars A and B respectively, ${{u}_{A}}\text{ and }{{u}_{B}}$ are the initial velocities of the cars A B and ${{v}_{A}}\text{ and }{{v}_{B}}$ are the final velocities of the cars.
We know that,
${{m}_{A}}={{m}_{B}}=1000kg$
${{u}_{A}}=10m/s$, which is given in the question
${{u}_{B}}=0m/s$, since the car B was at rest initially
${{v}_{A}}=0m/s$, since the car A came to rest after the collision
Now we can substitute these values in the equation and find velocity of the car B after collision.
$1000\times 10+1000\times 0=1000\times 0+1000\times {{v}_{B}}$
$\begin{aligned} & \Rightarrow 10000=1000{{v}_{B}} \\\ & \Rightarrow {{v}_{B}}=\dfrac{10000}{1000} \\\ \end{aligned}$
$\Rightarrow {{v}_{B}}=10m/s$
Hence we have the speed of car B after collision as 10 m/s.

Note:
When the car A collides with the car B, the momentum of car A will be transferred to B.
There will be no decrease in the velocity of the car A and the complete momentum will be transferred, i.e.
${{m}_{A}}{{v}_{A}}={{m}_{B}}{{v}_{B}}$
Since the mass of A and B is the same, we get
${{v}_{A}}={{v}_{B}}=10m/s$, since velocity of car A is 10 m/s
Thus we get the same solution.