Question

An automobile engine absorbs 1600J of heat from a hot reservoir and expels $1000{\text{J}}$ to a cold reservoir in each cycle. Find the maximum work done in each cycle.
A) $400{\text{J}}$
B) $500{\text{J}}$
C) $600{\text{J}}$
D) $450{\text{J}}$

Answer 1

According to the first law of thermodynamics, the heat supplied to a system is used to increase the internal energy of the system and to do work. The automobile engine resembles a heat engine that absorbs heat from a source to do some work and rejects the remaining heat to the sink.

Formula used:
The amount of work done by a heat engine is given by, $W = {Q_1} - {Q_2}$ where ${Q_1}$ is the heat absorbed from the source and ${Q_2}$ is the heat rejected to the sink after doing the work $W$.

Complete step by step answer:

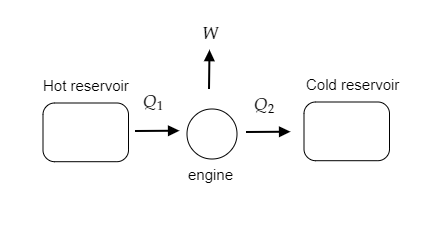
The above figure is a schematic representation of the working of the automobile engine.
In the problem at hand, heat is absorbed from a hot reservoir (or source) by an automobile engine. This absorbed heat is given to be ${Q_1} = 1600{\text{J}}$ .
The engine then does some work and rejects the remaining heat to the cold reservoir (or sink).
The heat rejected by the engine is given to be ${Q_2} = 1000{\text{J}}$ .
The first law of thermodynamics gives the work done by the automobile engine in one cycle as $W = {Q_1} - {Q_2}$ ----- (1)
Substituting for ${Q_1} = 1600{\text{J}}$ and ${Q_2} = 1000{\text{J}}$ in equation (1) we get, $W = 1600 - 1000 = 600{\text{J}}$ .

Thus the work done by the automobile engine is $W = 600{\text{J}}$. Hence the correct option is C.

Note:
The first law of thermodynamics is actually expressed as $\Delta Q = \Delta W + \Delta U$ where $\Delta W$ is the work done by the system and $\Delta U$ is the change in internal energy of the system. Here, after each cycle, the automobile engine comes back to its initial state and so the change in internal energy will be zero. Thus for an automobile engine, $W = \Delta Q$ . If no heat was rejected to the cold reservoir, then the entire heat absorbed from the hot reservoir would have been converted into useful work by the automobile engine and thus it would have an efficiency of 100%.