Question

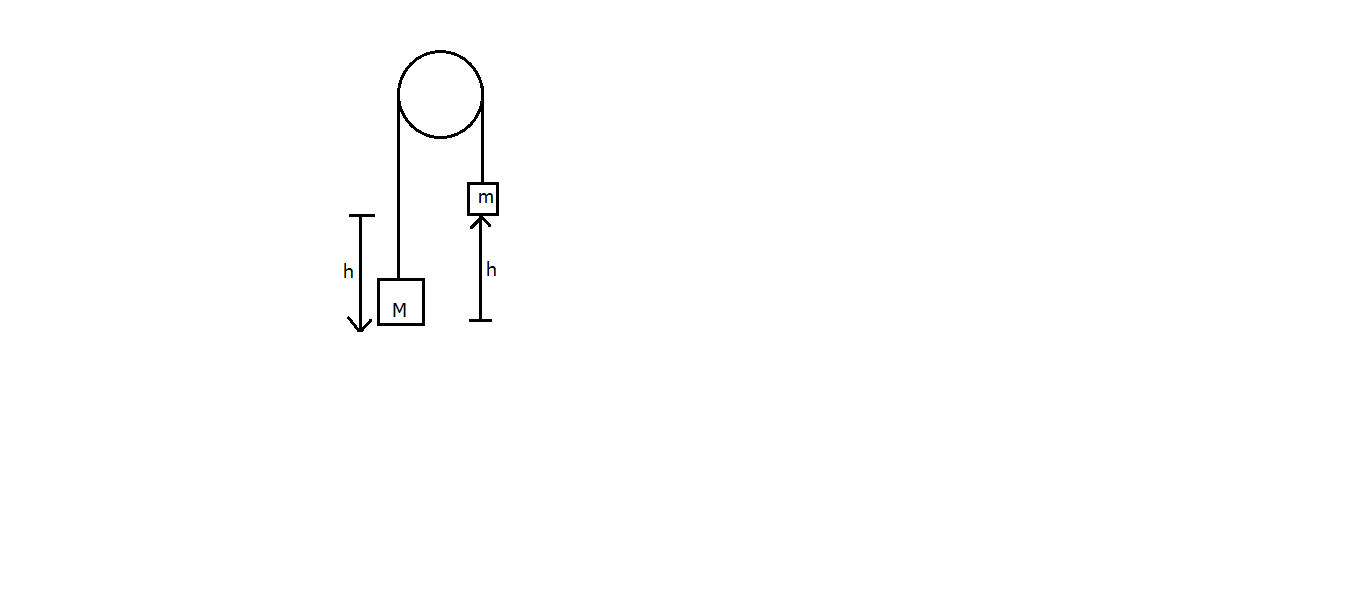
An Atwood machine (two masses connected via a cord that passes over a massless pulley) is set up with a $340g$ weight on one side and a $230g$ weight on the other.
Both masses start from rest, and when released the $340g$ weight falls through a distance of $0.50m$ while pulling the other weight up by the same amount. What is the average power output of the $340g$ weight on the $230g$ weight?
\left( A \right)0.525W \\\ \left( B \right)1.05W \\\ \left( C \right)1.31W \\\ \left( D \right)2.62W \\\ \left( E \right)None\ of\ the\ above \\\

Answer 1

Hint : To solve this question, we are going to first consider the forces on both the masses acting due to the tension and the gravity and then, from both the equations, the acceleration is found for both the masses, then the force on the mass $m$ from which we can find the work done and hence the power.
The tension and gravity give the total force
$T - Mg = - Ma$
The distance, $s$ covered by the mass, $M$ is given by
$s = u + \dfrac{1}{2}a{t^2}$
Power is given by $P = \dfrac{W}{t}$

Complete Step By Step Answer:
As from the diagram given in the question, the forces on the two masses are given by the relations
$T - Mg = - Ma$
And for the smaller mass $m$
$T - mg = ma$
From the both equations, we see that the value of tension equals
$- Ma + Mg = ma + mg$
Solving for the acceleration of the masses, we get
$a = \dfrac{{M - m}}{{M + m}}g$
Putting the values of the masses, $M$ and $m$ ,
$a = \dfrac{{340 - 230}}{{340 + 230}} \times 10 = \dfrac{{110}}{{570}} \times 10 = 1.929$
Therefore total force on the mass $M$ is
$F = Ma = 230 \times 1.929 = 443.67$
As it is given that the mass is displaced by the distance $0.50m$ , therefore, the work done is
$W = F \times s = 443.67 \times 0.50 = 221.835$
We know that the distance, $s$ covered by the mass, $M$ is given by
$s = u + \dfrac{1}{2}a{t^2}$
We know that the initial velocity of the mass $M$ is zero, so, the distance becomes
$s = \dfrac{1}{2}a{t^2} \Rightarrow t = \sqrt {\dfrac{{2s}}{a}}$
Now solving for the time, $t$ is
$t = \sqrt {\dfrac{{2 \times 0.50}}{{1.929}}} = 0.72s$
Thus, the average power output with which the weight $340g$ pulls $230g$
$P = \dfrac{W}{t} = \dfrac{{221.835 \times {{10}^{ - 3}}J}}{{0.72s}} = 0.308W$
Hence, none of the above options is correct, hence option $\left( E \right)None\ of\ the\ above$ is the correct answer.

Note :
The distance $h$ by which the mass $M$ comes down is equal to the distance by which the mass $m$ goes up, also the acceleration for both the masses is same, the force applied by the mass $M$ on the smaller mass performs the work done $W$ , which gives the final power with which the mass $M$ pulls the mass $m$ .