Question

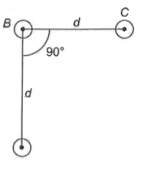
An arrangement of three parallel straight wires placed perpendicular to a plane of paper carrying the same current ‘I’ along the same direction is shown in figure. Magnitude of force per unit length on the middle wire ′B′ is given by

(A) $\dfrac{{{\mu _0}{i^2}}}{{\sqrt 2 \pi d}}$
(B) $\dfrac{{{\mu _0}{i^2}}}{{2\pi d}}$
(C) $\dfrac{{2{\mu _0}{i^2}}}{{\pi d}}$
(D) $\dfrac{{\sqrt 2 {\mu _0}{i^2}}}{{\pi d}}$

Answer 1

We can use Biot-savart law to get the magnetic field at some distance due to a conducting straight wire and use the relation between magnetic field and force to calculate the magnetic force per unit length.
Formula used:
$\overrightarrow F = i(\overrightarrow l \times \overrightarrow B )$

Complete step by step answer:
It is given that there are three wires kept perpendicular to the plane of paper, so we can use biot sarvart law to calculate magnetic fields due to these straight wires.
$B = \dfrac{{{\mu _0}}}{{2\pi }}\dfrac{i}{R}$gives the magnetic field B at distance R from a current carrying conductor
So magnetic field on point A will be ${B_A} = \dfrac{{{\mu _0}}}{{2\pi }}\dfrac{i}{d}$
And magnetic field on point C will be ${B_C} = \dfrac{{{\mu _0}}}{{2\pi }}\dfrac{i}{d}$
And we know that $\overrightarrow F = i(\overrightarrow l \times \overrightarrow B )$ where F is the force on the conductor of l length carrying I amount of current when placed in ‘B’ magnetic field.
Here, let us suppose the force on point B due A is $\overrightarrow {{F_{BA}}}$ so,
$\dfrac{{{F_{BA}}}}{l} = i{B_A} = i\dfrac{{{\mu _0}}}{{2\pi }}\dfrac{i}{d} = \dfrac{{{\mu _0}}}{{2\pi }}\dfrac{{{i^2}}}{d}$, we can find the direction by Fleming’s left hands rule we will get downward direction
suppose the force on point B due C is $\overrightarrow {{F_{BC}}}$ so,
$\dfrac{{{F_{BC}}}}{l} = i{B_C} = i\dfrac{{{\mu _0}}}{{2\pi }}\dfrac{i}{d} = \dfrac{{{\mu _0}}}{{2\pi }}\dfrac{{{i^2}}}{d}$ by Fleming’s left hands rule we will get the direction along BC
So, the net magnetic force per unit length will be ${F_{net}} = \sqrt {|{F_{BA}}{|^2} + |{F_{BC}}{|^2}} = \sqrt 2 \dfrac{{{\mu _0}}}{{2\pi }}\dfrac{{{i^2}}}{d} \approx \dfrac{{{\mu _0}}}{{\sqrt 2 \pi }}\dfrac{{{i^2}}}{d}$

Hence, the correct option is A

Note:
Fleming's left hand rule can be used to find the direction of force on a current carrying conductor when placed in a magnetic field. It states that when the fore-finger, the middle one and the thumb are placed mutually perpendicular to each other , where the fore-finger shows magnetic field direction , the middle finger shows the current flowing then the direction in which the thumb points will give the direction of magnetic force.