Question

An army pilot flying an aeroplane at an altitude of 1800 m observes some suspicious activity of two ships which are sailing towards it in the same directions and immediately reports it to the army chief. The angles of depression of the ships as observed from the aeroplane are $60^\circ$and $30^\circ$respectively.
(i)Find the distance between the two ships.
(ii)What value of the pilot is shown?

Answer 1

Here, we will first draw the diagram using the given information. We will use trigonometric ratios and substitute the given values in the formula to find the distance between the two ships approaching the aeroplane in the same direction.

Formula used:
We will use the formula $\tan \theta = \dfrac{{{\rm{opposite side}}}}{{{\rm{adjacent side}}}}$.

Complete step-by-step answer:
We will first draw the figure based on the given information.

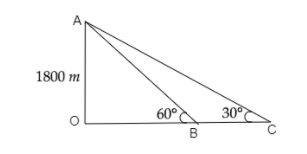
In the adjoining figure, let A be the position of the aeroplane, B and C be the positions of the approaching ships making angles $60^\circ$ and $30^\circ$ respectively. The altitude of the aeroplane is $OA = 1800$ m. We have to find the distance between the ships, i.e., length BC.
Let us first consider $\Delta OAB$.
$\tan 60^\circ = \dfrac{{OA}}{{OB}}$
Substituting $\tan 60^\circ = \sqrt 3$ and $OA = 1800$ m in the above equation, we get
$\Rightarrow \sqrt 3 = \dfrac{{1800}}{{OB}}$
On cross-multiplication, we get
$\Rightarrow OB = \dfrac{{1800}}{{\sqrt 3 }}$
We will now remove the radicals from the denominator.
Multiplying and dividing by $\sqrt 3$ on the RHS, we get
$\begin{array}{l} \Rightarrow OB = \dfrac{{1800}}{{\sqrt 3 }} \times \dfrac{{\sqrt 3 }}{{\sqrt 3 }}\\\ \Rightarrow OB = \dfrac{{1800\sqrt 3 }}{3}\end{array}$
Dividing the numerator by denominator, we get
$\Rightarrow OB = 600\sqrt 3$…………………………..$\left( 1 \right)$
Now, let us consider $\Delta OAC$. Therefore, we have,
$\tan 30^\circ = \dfrac{{OA}}{{OC}}$
Substituting $\tan 30^\circ = \dfrac{1}{{\sqrt 3 }}$ and $OA = 1800$ m in the above equation, we get
$\Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{1800}}{{OC}}$
On cross multiplication, we get
$OC = 1800\sqrt 3$…………………………..$\left( 2 \right)$
Now we will find the distance between the two ships which is equal to the BC. Therefore, we get
$BC = OC - OB$
Using equation $\left( 1 \right)$ and $\left( 2 \right)$, we have
$\Rightarrow BC = 1800\sqrt 3 - 600\sqrt 3$
Subtracting the terms, we get
$\Rightarrow BC = 1200\sqrt 3$ m
Hence,
(i) The distance between the two ships is $1200\sqrt 3$ m.
(ii) The quality of the pilot that is demonstrated here is the environmental awareness that all pilots must possess.

Note: In the above question, we have used the trigonometric ratio ‘$\tan$’ because we are only dealing with the opposite side and the adjacent side (with respect to the angle under consideration). Instead of ‘$\tan$’, the ratio ‘$\cot$’ can also be used since ‘$\cot$’ also relates the opposite side and the adjacent side. Here, we have to also write the value of the pilot. For that, we will analyse the question and apply our reasoning ability to answer the question.