Question

An arch is in the form of semi-eclipse. It is 8 m wide and 2 m high at the center. Find the height of the arch at a point 1.5 m from one end.

Answer 1

In mathematics, an ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. As such, it generalizes a circle, which is the special type of ellipse in which the two focal points are the same.

Complete step by step solution:
According to the question, the above can be represented as the following diagram.

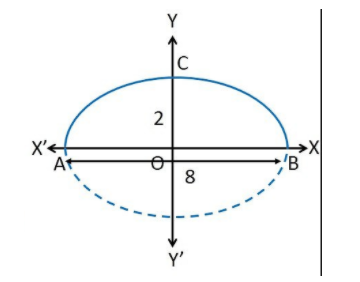
Let the length of the major axis or the width of the half ellipse be AB
And the height of the semi ellipse be CO
Thus, AB = 8 m
And CO = 2 m
And since we know that length of the major axis is
$= 2a = 8m \\\ \Rightarrow a = 4m \\\$
And $b = 2m$
The equation of the semi ellipse will be of the form
$\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$where a is semi major axis and b will be the semi minor axis
Thus accordingly a = 4m and b = 2m
Thus the equation becomes,
$\dfrac{{{x^2}}}{{{4^2}}} + \dfrac{{{y^2}}}{{{2^2}}} = 1 \\\ \Rightarrow \dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{4} = 1 \\\$
Now,
Let P be a point on major axis such that AP = 1.5m
And, draw $PQ \bot AO$
Thus OP $= (4 - 1.5)m = 2.5m$
Thus the x co-ordinate of Q will be $- 2.5m$
Now, on substituting the value of x with $- 2.5m$ in the equation of ellipse we will get,

$$\dfrac{{{{( - 2.5)}^2}}}{{16}} + \dfrac{{{y^2}}}{4} = 1 \\\ \Rightarrow \dfrac{{6.25}}{{16}} + \dfrac{{{y^2}}}{4} = 1 \\\ \Rightarrow \dfrac{{{y^2}}}{4} = 1 - \dfrac{{6.25}}{{16}} \\\ \Rightarrow {y^2} = 4 \times (1 - \dfrac{{6.25}}{{16}}) \\\ \Rightarrow {y^2} = 4(\dfrac{{9.75}}{{16}}) \\\ \Rightarrow {y^2} = 2.4375 \\\ \Rightarrow y = \sqrt {2.4375} \\\ \Rightarrow y = 1.56(approx)(\because y > 0) \\\ \therefore PQ = 1.56m \\\$$

Thus the height of the arch at a point 1.5 m from one end is = 1.56 m.

Note: While solving these types of questions always figure out that on what axis the major axis will be made and vice versa.