Question

An arch is in the form of a parabola with its axis vertical. The arch is $10$ m high and $5$ m wide at the base. How wide is it $2$ m from the vertex of the parabola.

Answer 1

A parabola is defined as a set of points that are equidistant from a directrix, which is a fixed straight line and the focus. If the parabola has directrix as the x-axis, and the focus is $(a,0)$ , then the equation of the parabola is given by ${y^2} = 4ax$ and if the parabola has directrix as the y-axis, and the focus is $(0,a)$ , then the equation of the parabola is given by ${x^2} = 4ay$ . If any point lies on the parabola, it means that it will satisfy the equation of the given parabola.

Complete step by step answer:
It is given that an arch is in the form of a parabola with its axis vertical and the arch is $10$ m high and $5$ m wide at the base. So, to illustrate it in the form of a figure, let us take the vertex of this parabola to be at origin $(0,0)$ . Then it will form a parabola such that its vertical is at origin and the directrix is along the negative y-axis. To represent it diagrammatically, we have,

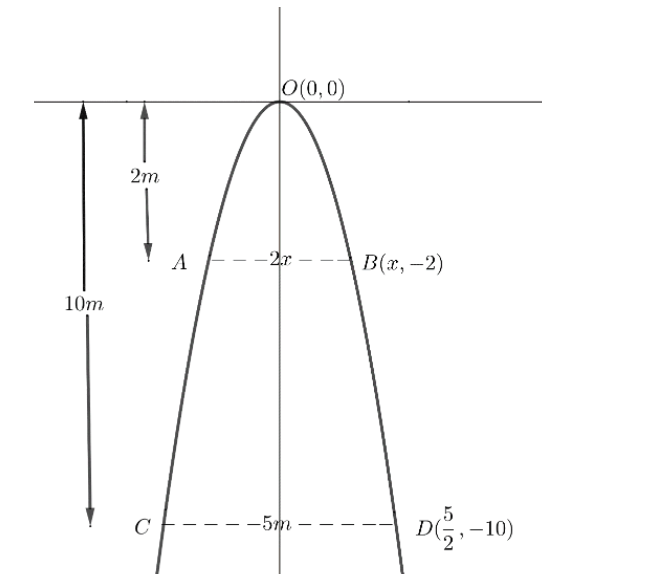
From the given figure, we see that the equation of the parabola opening on the negative y axis is given by ${x^2} = - 4ay$ .
We need to determine the value of the focus, that is $a$ for the given parabola, to proceed further.
Since the point $D\left( {\dfrac{5}{2}, - 10} \right)$ lies on the parabola, it will satisfy the given equation of the parabola.
Substitute $x = \dfrac{5}{2},y = - 10$ in the equation of parabola ${x^2} = - 4ay$ .
${\left( {\dfrac{5}{2}} \right)^2} = - 4a( - 10)$
$\dfrac{{25}}{4} = 40a$
$a = \dfrac{{25}}{{4 \times 40}} = \dfrac{5}{{32}}$
So, the equation of the given parabola becomes,
${x^2} = - 4\left( {\dfrac{5}{{32}}} \right)y$
${x^2} = - \dfrac{5}{8}y$
Now to determine the width of the arch, when measured $2$ m from the vertex of the parabola, say the width is $2x$ m. From the given parabola figure, we need to determine the value of $x$ , when measured $2$ m away from the x-axis. That is, we are required to determine the coordinates of the point $B(x, - 2)$ . Here, $- 2$ represent that the point $B$ is towards the negative side of the y-axis, hence $y = - 2$ .
Since this point $B$ lies on the parabola, it will satisfy the equation of the given parabola represented by ${x^2} = - \dfrac{5}{8}y$ .
Substitute $y = - 2$ in this equation ,
${x^2} = - \dfrac{5}{8}( - 2)$
${x^2} = \dfrac{5}{4}$
Taking the square root on both sides of the equation
$x = \pm \sqrt {\dfrac{5}{4}}$
$x = \pm \dfrac{{\sqrt 5 }}{2}$
Since the width represents the length, we will not consider the negative value of $x$ , hence $x = \dfrac{{\sqrt 5 }}{2}$.
Now, since the width is $2x$ m, so
$2x = 2 \times \dfrac{{\sqrt 5 }}{2} = \sqrt 5 \approx 2.23$
So, the width of the arc is approximately $2.23$ when measured $2$ m from the vertex of the parabola.

Note:
For a parabola having the equation ${x^2} = 4ay$ , the axis of symmetry is the y-axis and vertex lie on the origin. And for a parabola having the equation ${y^2} = 4ax$ , the axis of symmetry is the x-axis and vertex lie on the origin. If the value of $a$ is positive, then the parabola will have focus on the positive side of the axis of symmetry, and if the value of $a$ is negative, then the parabola will have focus on the negative side of the axis of symmetry.