Question

An ant crawls $1$ cm north, $2$ cms west, $3$ cms south, $4$ cms east and $5$ cms north and so on, at $1$ centimeter per second. Each segment is $1$ centimeter longer than the preceding one, and at the end of a segment, the ant makes a left turn. In which direction is the ant moving $1$ minute after the start?
A. South
B. North
C. East
D. West

Answer 1

In order to find the answer to the above question, we will use arithmetic progression (AP). It refers to the sequence of numbers such that the difference between the consecutive terms is constant. A diagram can be drawn to clearly understand the question and it will make the question easier to solve.

Formula used:
The formula of arithmetic progression will be used to solve this question.
The formula is: ${S_n} = \dfrac{n}{2}\left[ {2a + \left( {n - 1} \right)d} \right]$ , in this formula $a$ refers to the first term of the progression and $d$ is the difference between the two consecutive terms.
The second formula which will be used to solve this question is of quadratic equations.
$x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$

Complete step by step solution:
Now we know,
The ant always travels $\left( {4k + 1} \right)$ cm North, $\left( {4k + 2} \right)$ West, $\left( {4k + 3} \right)$ cm South and $\left( {4k + 4} \right)$ East.
Therefore, the distance travelled by the ant in $1$ min is $60 \times 1cm = 60cm$ .
From the above statements we get the following AP: $1,2,3,4........$
To solve this arithmetic progression, we will use the formula mentioned above.
${S_n} = \dfrac{n}{2}\left[ {2a + \left( {n - 1} \right)d} \right]$ , here $a = 1$ and $d = 1$ .
So,
$60 = \dfrac{n}{2}\left[ {2 \times 1 + \left( {n - 1} \right) \times 1} \right]$
On cross multiplication, we get,

$$\Rightarrow 120 = n\left[ {2 + n - 1} \right] \\\ \Rightarrow 120 = n\left[ {n + 1} \right] \\\ \Rightarrow 120 = {n^2} + n \\\$$

Take all the terms on right side of the equation, we get,
${n^2} + n - 120 = 0$
Now to solve this quadratic equation, we will use the formula, $x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$ , here $x$ is replaced by $n$ , $a = 1,b = 1$ and $c = - 120$ .
$n = \dfrac{{ - 1 \pm \sqrt {{1^2} - 4\left( 1 \right)\left( { - 120} \right)} }}{{2\left( 1 \right)}}$
$\Rightarrow n = \dfrac{{ - 1 \pm \sqrt {1 + 480} }}{2}$
On further solving, we get,
$\Rightarrow n = \dfrac{{ - 1 \pm \sqrt {481} }}{2}$
$= \dfrac{{ - 1 \pm 22}}{2}$
$= \dfrac{{21}}{2}$ .
This can be written as $10\dfrac{1}{2}$ .
We will take $n = 11$ .
Therefore, ${a_{11}} = 1 + 10 \times 1$
$= 11$ .
This can be written as $11 = 4 \times 2 + 3$ .

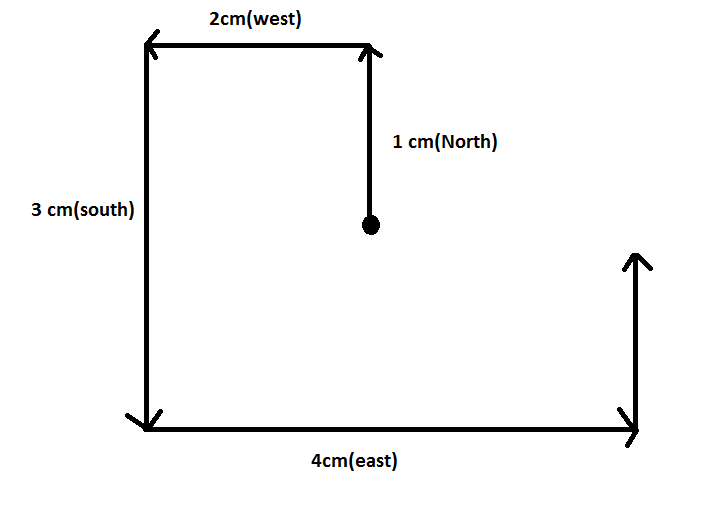
So, the correct answer is Option A.

Note: To solve such sums related to arithmetic progression (AP), you need to always remember the formula mentioned above for AP, ${S_n} = \dfrac{n}{2}\left[ {2a + \left( {n - 1} \right)d} \right]$ . In the above solution, we have used a formula, $x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$ , for solving the quadratic equation. This formula helps when the calculations are either long or tricky.