Question

An annular ring of internal and outer radii r and R respectively oscillates in a vertical plane about a horizontal axis perpendicular to its plane and passing through a point on its outer edge. Calculate its time period and show that the length of an equivalent simple pendulum is $\dfrac{{3R}}{2}$ as $r \to 0$ and 2R as $r \to R$.

Answer 1

Here we have to find the time period and length. Apply the relation between angular and linear force $\tau = r \times F$ where $\tau$= angular force; $r$= distance; F = linear force and then for angular acceleration $\alpha = - {\omega ^2}\theta$ where $\alpha$= angular acceleration; $\omega$= angular velocity and solve.

Complete step by step solution:

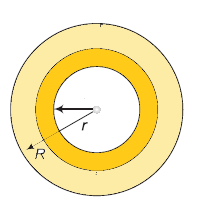
Step 1:
When the ring is rotated through an angle $\theta$.
We know the torque in terms of linear force;
$\tau = r \times F$;
$\tau = rF\sin \theta$;
Put the value of F = mg in the above relation:
$\tau = mgr\sin \theta$;
Now,
$\tau = mgr\sin \theta = - mgr\theta$;
Here $\tau = I\alpha$; …($I$= Moment of Inertia; $\alpha$= Angular acceleration)
Put the value of torque in the above relation:
$I\alpha = - mgr\theta$;
$\alpha = - \dfrac{{mgr\theta }}{I}$;
We know the relation between angular acceleration and angular velocity:
$- {\omega ^2}\theta = - \dfrac{{mgr\theta }}{I}$;
Solve for $\omega$= Angular velocity;
$\omega = \sqrt {\dfrac{{mgr}}{I}}$;

Step 2: We know the relation between time period and angular velocity:
$T = \dfrac{{2\pi }}{\omega }$ ;
Put the value of $\omega = \sqrt {\dfrac{{mgr}}{I}}$in the above relation:
$T = \dfrac{{2\pi }}{{\sqrt {\dfrac{{mgr}}{I}} }}$;
Now,
$T = 2\pi \sqrt {\dfrac{I}{{mgr}}}$;
Now for a circular disk the moment of inertia is:
$I = \dfrac{{M{r^2}}}{2}$;
Here we have a ring which is equal to 2 circular disks, the moment of inertia would be:
$I = \dfrac{{{M_1}{R^2}}}{2} - \dfrac{{{M_2}{R^2}}}{2}$;
Now the Mass of the whole area of ring M would be:
$M = \sigma \pi ({R^2} - {r^2})$ ; ….($\sigma$= Mass per unit area)
From here we can find out the Mass per unit area
$\dfrac{M}{{\pi ({R^2} - {r^2})}} = \sigma$;
Similarly, mass for first disk would be:
${M_1} = \sigma \pi {R^2}$;
Put the value of $\sigma$in the above equation:
${M_1} = \dfrac{M}{{\pi ({R^2} - {r^2})}}\pi {R^2}$;
${M_1} = \dfrac{{M{R^2}}}{{({R^2} - {r^2})}}$;
The same would be applicable for disk 2:
${M_2} = \sigma \pi {r^2}$;
${M_2} = \dfrac{{M{r^2}}}{{({R^2} - {r^2})}}$;
Put the value of ${M_1}\& {M_2}$ in $I = \dfrac{{{M_1}{R^2}}}{2} - \dfrac{{{M_2}{R^2}}}{2}$;
$I = \dfrac{{M{R^4}}}{{2\left( {{R^2} - {r^{^2}}} \right)}} - \dfrac{{M{r^4}}}{{2\left( {{R^2} - {r^{^2}}} \right)}}$;
The formula for time period is:
$T = 2\pi \sqrt {\dfrac{I}{{mgr}}}$ ;
(Here $I$= moment of inertia; m = mass; g = gravitational acceleration; T = time period)
Put the value of Moment of Inertia in the above equation:
$T = 2\pi \sqrt {\dfrac{{\dfrac{{M{R^4}}}{{2\left( {{R^2} - {r^{^2}}} \right)}} - \dfrac{{M{r^4}}}{{2\left( {{R^2} - {r^{^2}}} \right)}}}}{{mgr}}}$;
$T = 2\pi \sqrt {\dfrac{{\dfrac{M}{{2\left( {{R^2} - {r^{^2}}} \right)}}\left( {{R^4} - {r^4}} \right)}}{{mgR}}}$;
Simplify the above equation:
$T = 2\pi \sqrt {\dfrac{{\dfrac{M}{2}\left( {{R^2} + {r^{^2}}} \right) + {R^2}}}{{mgR}}}$;
Here M = m; so, they will cancel out:
$T = 2\pi \sqrt {\dfrac{{\dfrac{1}{2}\left( {{R^2} - {r^{^2}}} \right) + {R^2}}}{{gR}}}$
Again, simplify the equation:
$T = 2\pi \sqrt {\dfrac{{\dfrac{{3R}}{2} + \dfrac{{{r^2}}}{{2R}}}}{g}}$;

Step 3:
The length would be:
${l_{eff}} = \dfrac{{3R}}{2} + \dfrac{{{r^2}}}{{2R}}$;
At $r \to 0$ ;
${l_{eff}} = \dfrac{{3R}}{2}$;
At $r \to R$:
${l_{eff}} = \dfrac{{3R}}{2} + \dfrac{{{R^2}}}{{2R}}$;
Do the needed calculation:
${l_{eff}} = \dfrac{{4R}}{2}$;
The length would be:
${l_{eff}} = 2R$;

The time period is $T = 2\pi \sqrt {\dfrac{{\dfrac{{3R}}{2} + \dfrac{{{r^2}}}{{2R}}}}{g}}$ and the effective length is At $r \to 0$,${l_{eff}} = \dfrac{{3R}}{2}$; At $r \to R$,${l_{eff}} = 2R$.

Note: It is a very lengthy process go step by step, first write the relation between transitional and rotational force then write the relation between angular acceleration and torque then find out the moment of inertia after that put the value of M.I in the formula for time period and solve.