Question

An annular disk has an inner and outer radius ${R_1}$ and ${R_2}$ respectively. A charge is uniformly distributed. Surface charge density is $\sigma$. Find the electric field at any point distant y along the axis of the disk.
A) $\dfrac{\sigma }{{2{\varepsilon _o}}}$
B) $\dfrac{{\sigma y}}{{2{\varepsilon _o}({R_2} - {R_1})}}$
C) $\dfrac{{\sigma y}}{{2{\varepsilon _o}}}\left[ {\dfrac{1}{{\sqrt {{R_1}^2 + {y^2}} }} - \dfrac{1}{{\sqrt {{R_2}^2 + {y^2}} }}} \right]$
D) $\dfrac{{\sigma y}}{{2{\varepsilon _o}}}\log \dfrac{{{R_2} + y}}{{{R_1} + y}}$

Answer 1

Here we have to imagine a hypothetical ring of radius X and thickness dx, the hypothetical ring is inside the ring. We have to find the electric field of the hypothetical ring first and then we have to integrate the electric field to get the electric field of the real ring on the point p on the y-axis.

Formula used:
The formula for finding out the coefficient of performance is given below.
$E = \dfrac{{Kqy}}{{{{({x^2} + {y^2})}^{3/2}}}}$
Here,
$E$= Electric field
$K$= Proportionality constant ($9 \times {10^9}$ $N$ ${m^2}/{C^2}$)
$q$= Charge
$x$= Distance in the direction of the x axis.
$y$= Distance in the direction of y axis
The formula for charge on the hypothetical ring is
dq = $\sigma$ $\times$ 2πx;
$\sigma$= Surface charge density.
$x$ = Radius of the hypothetical ring
$2πx$ = Circumference of the hypothetical ring.

Complete step by step answer:
Step 1: Look at the below picture. Here, apart from the Big ring whose radius is ${R_1}$ and ${R_2}$. We have to draw a hypothetical ring whose radius is x and thickness is dx. We have to find the charge on the hypothetical ring.

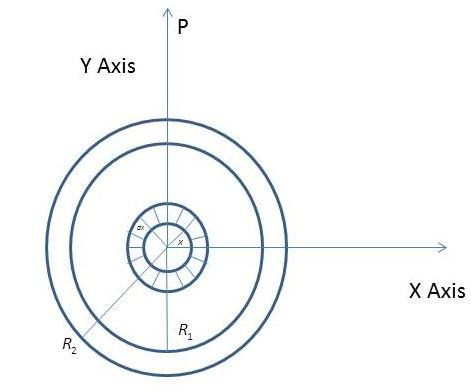
The charge on the hypothetical ring is
dq = $\sigma$× 2πx;
Now, we know the electric field due to a ring, which is
$E = \dfrac{{Kqy}}{{{{({x^2} + {y^2})}^{3/2}}}}$
So, for a small charge dq, the equation becomes,
$E = \dfrac{{Kdqy}}{{{{({x^2} + {y^2})}^{3/2}}}}$
Put the value of dq in the above equation
$E = \dfrac{{K(\sigma \times 2\pi x).y}}{{{{({x^2} + {y^2})}^{3/2}}}}$

Step 2: Calculating the total electric field of the ring by integrating the equation.
$E = \dfrac{{(\sigma \times 2\pi x).y}}{{4\pi {\varepsilon _o}{{({x^2} + {y^2})}^{3/2}}}}$; (Here k =$\dfrac{1}{{4\pi {\varepsilon _o}}}$=$9 \times {10^9}$)
After solving the above equation we get
$E = \dfrac{{\sigma. x.y}}{{2{\varepsilon _o}{{({x^2} + {y^2})}^{3/2}}}}$
Now, we integrate the equation from ${R_1}$to${R_2}$
$E = \dfrac{{\sigma y}}{{2{\varepsilon _o}}}\int_{{R_1}}^{{R_2}} {\dfrac{x}{{{{({x^2} + {y^2})}^{3/2}}}}} dx$
Let ${x^2} + {y^2}$=${p^2}$;
Now differentiate ${x^2}$ w.r.t x and ${p^2}$w.r.t p, we get
${x^2} + {y^2}$=${p^2}$; …. ($\dfrac{{d{x^n}}}{{dx}} = n{x^{n - 1}}$)
Differentiate each variable,
$\dfrac{{d{x^2}}}{{dx}} + \dfrac{{d{y^2}}}{{dx}} = \dfrac{{d{p^2}}}{{dp}}$; ….($\dfrac{{d{x^2}}}{{dx}} = 2x$); ($d{x^2} = 2xdx$)
Here$\dfrac{{d{y^2}}}{{dx}} = 0$; because of a different variable in the numerator,
$2x\,dx + 0 = 2p\,dp$;
$2x\,dx = 2p\,dp$;
Here, we have established a relation between xdx and pdp.
Now, put ${x^2} + {y^2}$=${p^2}$in the given below equation,
$E = \dfrac{{\sigma y}}{{2{\varepsilon _o}}}\int_{{R_1}}^{{R_2}} {\dfrac{x}{{{{({x^2} + {y^2})}^{3/2}}}}} dx$
Write the above equation in terms of $p$,
$E = \dfrac{{\sigma y}}{{2{\varepsilon _o}}}\int_{{R_1}}^{{R_2}} {\dfrac{p}{{{{({p^2})}^{3/2}}}}} dp$
solving the above equation,
$E = \dfrac{{\sigma y}}{{2{\varepsilon _o}}}\int_{{R_1}}^{{R_2}} {\dfrac{p}{{{p^{(3)}}}}} dp$
Simplify the above equation
$E = \dfrac{{\sigma y}}{{2{\varepsilon _o}}}\int_{{R_1}}^{{R_2}} {\dfrac{1}{{{p^{(2)}}}}} dp$ ….($\int {{p^{( - n)}}dp = \dfrac{{{p^{( - n) + 1}}}}{{( - n) + 1}}}$)
Solving integration,
$E = \dfrac{{\sigma y}}{{2{\varepsilon _o}}}\left[ {\dfrac{{{p^{( - 2) + 1}}}}{{( - 2) + 1}}} \right]_{{R_1}}^{{R_2}}$
Simplify further,
$E = \dfrac{{\sigma y}}{{2{\varepsilon _o}}}\left[ { - {p^{ - 1}}} \right]_{{R_1}}^{{R_2}}$
Put the value of p i.e. p =${( - \sqrt {{x^2} + {y^2}} )^{ - 1}}$
$E = \dfrac{{\sigma y}}{{2{\varepsilon _o}}}\left[ {{{( - \sqrt {{x^2} + {y^2}} )}^{ - 1}}} \right]_{{R_1}}^{{R_2}}$
$E = \dfrac{{\sigma y}}{{2{\varepsilon _o}}}\left[ {\dfrac{1}{{( - \sqrt {{x^2} + {y^2}} )}}} \right]_{{R_1}}^{{R_2}}$
Put the upper limit (${R_2}$) in place of x and then put the lower limit (${R_1}$) in place of $x$. Add the two terms together.
$E = \dfrac{{\sigma y}}{{2{\varepsilon _o}}}\left[ { - \dfrac{1}{{(\sqrt {{R_2}^2 + {y^2}} )}} + \dfrac{1}{{(\sqrt {{R_1}^2 + {y^2}} )}}} \right]$

The electric field at any point distant y along the axis of the disk is $E = \dfrac{{\sigma y}}{{2{\varepsilon _o}}}\left[ { - \dfrac{1}{{(\sqrt {{R_2}^2 + {y^2}} )}} + \dfrac{1}{{(\sqrt {{R_1}^2 + {y^2}} )}}} \right]$. Hence option (C) is correct.

Note:
The equation $E = \dfrac{{\sigma y}}{{2{\varepsilon _o}}}\int_{{R_1}}^{{R_2}} {\dfrac{x}{{{{({x^2} + {y^2})}^{3/2}}}}} dx$ is of complex nature. Kindly be careful while doing the integration. Here we have to solve complicated integration as well as complicated variables, to make it simple put the complicated variable into a single variable and then solve for the integration.