Question

An amusement park ride consists of a large vertical cylinder that spins about its axis fast enough that any person inside is held up against the wall when the floor drops away. The coefficient of static friction between person and wall is ${\mu _s}$​, and the radius of the cylinder is $R$.

A. Show that the maximum period of revolution necessary to keep the person from falling is $T = \sqrt {\dfrac{{4{\pi ^2}R{\mu _s}}}{g}}$
B. Obtain a numerical value for $T$, taking $R = 4m$ and ${\mu _s} = 0.400$. How many revolutions per minute does the cylinder make?
C. If the rate of revolution of the cylinder is made to be somewhat large, what happens to the magnitude of each one of the forces acting on the person? What happens to the motion of the person?
d. If instead the cylinder's rate of revolution is made to be somewhat smaller, what happens to the magnitude of each one of the forces acting on the person. What happens to the motion of the person?

Answer 1

To solve (A) part of the question, we find all the forces acting on the body just so that the person is held against the wall. We find the normal force using a centrifugal force formula, which is further used to find the friction force between the wall and the person. We equate this with the weight of the person to find the time period. For the (B) part we simply substitute the values given in the question in the formula found earlier to get the solution. The units are then converted to per minute. Part (C) and (D) we apply the conditions given in the question to see how the forces vary.

Complete step by step answer:
(A)
The free-body diagram of the person is

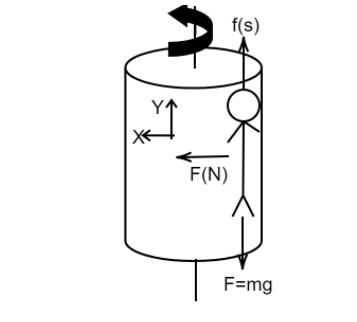
For the person to be held against the wall the friction force action should be equal to the weight of the person.
Normal force action on the body is equal to the centrifugal force. The normal force is acting inwards.
${F_N} = \dfrac{{m{v^2}}}{R}$
Here, normal force is represented by ${F_N}$
Radius of the cylinder is represented by $R$
Mass of the person is represented by $m$
Velocity with which the person is being revolved is represented by $v$
Velocity is also equal to
$v = \dfrac{D}{t} = \dfrac{{2\pi R}}{T}$
Using this in normal force
${F_N} = \dfrac{m}{R} \times {(\dfrac{{2\pi R}}{T})^2}$
$\Rightarrow {F_N} = \dfrac{{4{\pi ^2}Rm}}{{{T^2}}}$
Friction force is equal to
${f_s} = {\mu _s}{F_N}$
$\Rightarrow {f_s} = {\mu _s} \times \dfrac{{4{\pi ^2}Rm}}{{{T^2}}}$
Here, Coefficient of friction is represented by ${\mu _s}$
Friction force acting upwards is represented by ${f_s}$
Weight of the person action downwards is equal to
$F = mg$
Here,
Weight of the person is represented by $F = mg$
Gravitational force is represented by $g$
From the friction force and weight balance equation, for the person to be held against the wall
${f_s} = F$
$\Rightarrow {\mu _s} \times \dfrac{{4{\pi ^2}Rm}}{{{T^2}}} = mg$
$\Rightarrow {T^2} = \dfrac{{{\mu _s}4{\pi ^2}R}}{g}$
$\therefore T = \sqrt {\dfrac{{{\mu _s}4{\pi ^2}R}}{g}}$
Hence
$T = \sqrt {\dfrac{{{\mu _s}4{\pi ^2}R}}{g}}$
(B)
From the question
${\mu _s} = 0.400$
$R = 4m$
$g = 10$
Substituting in the formula of time period we get
$T = \sqrt {\dfrac{{{\mu _s}4{\pi ^2}R}}{g}}$
$\Rightarrow T = \sqrt {\dfrac{{0.4 \times 4{\pi ^2} \times 4}}{g}}$
$\Rightarrow T = \dfrac{{2\pi \times 4}}{{10}} = 2.50rev/s = 2.50 \times 60rev/\min$
$\therefore T = 150rev/\min$
(C) The gravitational force remains constant. (Static friction adjusts to support the weight) hence static friction and weight of a person are equal. The normal force increases. The person remains in motion held against the wall.
(D The gravitational force remains constant. Normal and friction forces decrease. The person slides relative to the wall and down the floor because the condition given is below the minimum centrifugal force required to keep the person against the wall.

Note: We can see that the gravitational force is always constant and nothing can change it. If the person is living down then it means the weight of the person is greater than the friction force acting between the person and the wall. Otherwise, the two forces are equal and the person is held against the wall.