Question

An amount of 19 g of molten $SnCl_2$ is electrolysed for some time. Inert electrodes are used. 1.19 g of tin is deposited at the cathode. No substance is lost during electrolysis. If the ratio of the masses of $SnCl_2$ and $SnCl_4$ after electrolysis is $x:261$, the value of $x$ is (Sn = 119)

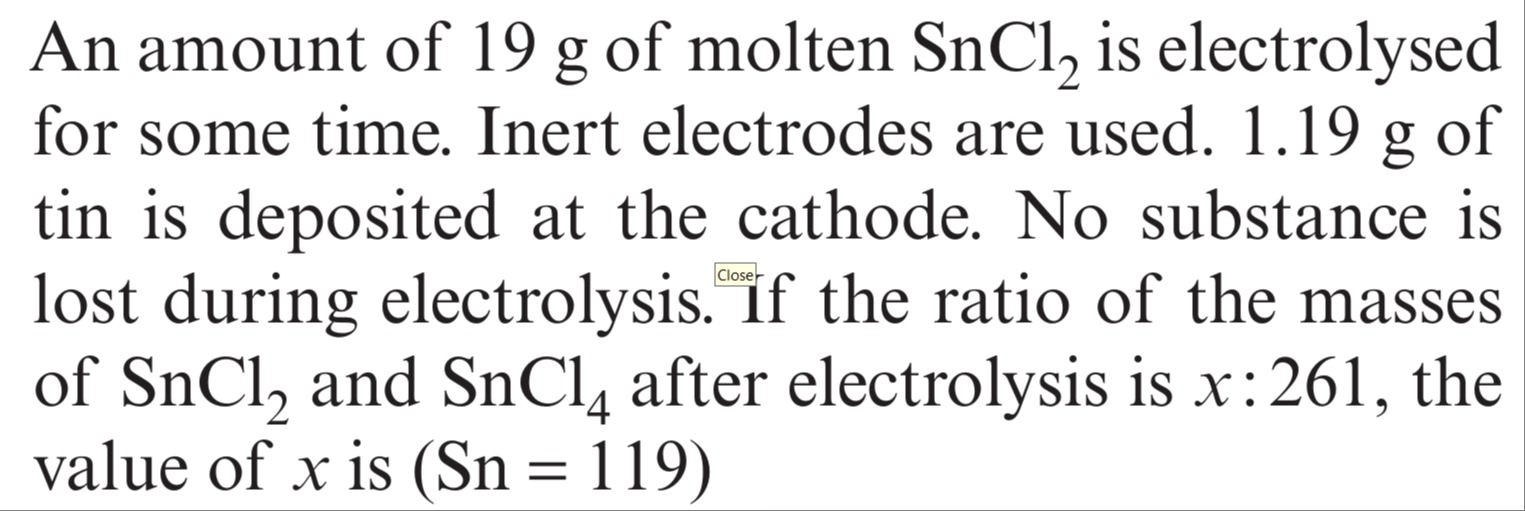
• A. 1520
• B. 15.20
• C. 261
• D. 119

Answer 1

Answer: (A)

1520

Answer 2

The electrolysis of molten $SnCl_2$ results in the formation of tin metal at the cathode and $SnCl_4$ at the anode, via the disproportionation reaction: $2SnCl_2 \rightarrow SnCl_4 + Sn$

From the stoichiometry: 2 moles of $SnCl_2$ (2 $\times$ 190 g = 380 g) yield 1 mole of $SnCl_4$ (261 g) and 1 mole of $Sn$ (119 g).

Given that 1.19 g of tin is deposited: Moles of Sn deposited = $\frac{1.19 \text{ g}}{119 \text{ g/mol}} = 0.01$ mol.

Based on the stoichiometry:

1. Mass of $SnCl_4$ produced: Since 1 mole of Sn is produced with 1 mole of $SnCl_4$, 0.01 mol of $SnCl_4$ is produced. Mass of $SnCl_4$ = $0.01 \text{ mol} \times 261 \text{ g/mol} = 2.61$ g.

2. Mass of $SnCl_2$ reacted: Since 2 moles of $SnCl_2$ react to produce 1 mole of Sn, 0.02 mol of $SnCl_2$ reacted. Mass of $SnCl_2$ reacted = $0.02 \text{ mol} \times 190 \text{ g/mol} = 3.80$ g.

3. Mass of $SnCl_2$ remaining: Initial mass of $SnCl_2$ = 19 g. Mass of $SnCl_2$ remaining = $19 \text{ g} - 3.80 \text{ g} = 15.20$ g.

4. Determine the ratio: The ratio of the masses of $SnCl_2$ and $SnCl_4$ after electrolysis is given as $x:261$. This ratio compares the remaining $SnCl_2$ to the produced $SnCl_4$. The calculated ratio is $15.20 \text{ g} : 2.61 \text{ g}$.

5. Solve for x: We set up the proportion: $\frac{15.20}{2.61} = \frac{x}{261}$ $x = \frac{15.20 \times 261}{2.61} = 15.20 \times 100 = 1520$.