Question

An ammeter reads upto 1 ampere. Its internal resistance is 0.81 ohm. To increase the range to 10 A, the value of the required shunt is
A) $0.03\Omega$
B) $0.3\Omega$
C) $0.9\Omega$
D) $0.09\Omega$

Answer 1

Hint: A shunt is connected parallel to an ammeter in order to enable the ammeter to measure higher currents. So the shunt that is being connected should have a resistance that will allow the ammeter to measure a particular current range.

Complete step by step answer:

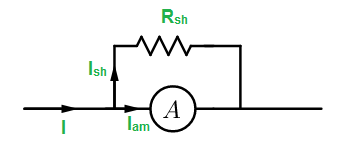
In the problem, it is given that the internal resistance of the ammeter is $0.81\Omega$ and the max current the ammeter can read is 1 ampere. We need to increase this 1 ampere range to 10 A. In order to do that we need to connect a shunt parallel to the ammeter.
Let $\text{I}$ be the maximum current in the range we need to set and ${{i}_{g}}$ be the current flowing through the ammeter. So the current flowing through the shunt is given by $I-{{i}_{g}}$.
Since the ammeter is connected in parallel with the shunt, the voltage drop across each of them is same, so we can write,
${{\text{I}}_{\text{sh}}}{{\text{R}}_{\text{sh}}}={{\text{I}}_{\text{am}}}{{\text{R}}_{\text{am}}}$
${{\text{I}}_{\text{sh}}}$ is the current across the shunt. We have calculated it as $I-{{i}_{g}}$.
${{\text{R}}_{\text{sh}}}$ is the resistance of the shunt. Which we need to find out.
${{\text{I}}_{am}}$ is the current across the ammeter. We have taken it as ${{i}_{g}}$.
${{\text{R}}_{am}}$ is the internal resistance of the ammeter.
So the resistance of the shunt can be written as,
${{R}_{sh}}=\dfrac{{{I}_{am}}{{R}_{am}}}{{{I}_{sh}}}=\dfrac{{{i}_{g}}{{R}_{am}}}{\left( I-{{i}_{g}} \right)}$
Substituting the values of ${{i}_{g}}$,${{\text{I}}_{am}}$,${{\text{R}}_{am}}$ we get,
${{R}_{sh}}=\dfrac{1A\times 0.81\Omega }{\left( 10A-1A \right)}$
${{R}_{sh}}=0.09\Omega$

Note:
In the absence of a shunt, higher current can damage an ammeter which is supposed to measure low currents. Higher currents can produce the heating effect, which will result in the burning of the ammeter coil.
A shunt provides a low resistance path for the current to flow. For proper working, the resistance of the shunt should not change with temperature.