Question
Question: An ammeter of resistance 0.8 \(\Omega \) can measure current up to 1.0A (i) What must be the value o...
An ammeter of resistance 0.8 Ω can measure current up to 1.0A (i) What must be the value of shunt resistance to enable the ammeter to measure current up to 5A. (ii) What is the combined resistance of the ammeter and the shunt?
Solution
Hint- The ammeter is designed for measuring the low current. For measuring the heavy current, the shunt is connected in parallel to the ammeter. Due to the low strength course, the important part of the measuring current passes into the shunt and few amounts of current passes through the ammeter.
Complete step-by-step answer:
The shunt attaches parallel to the meter, which allows the voltage to fall over the meter and the shunt remains the same. The shunt therefore does not affect the rotation of the pointer.
Given
Resistance of the ammeter RA=0.8Ω
Current rating = 1A
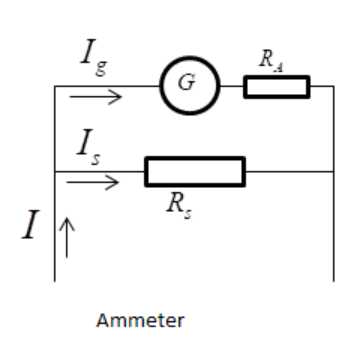
i) Value of the shunt resistance to measure 5 A current
The value of shunt resistance is calculated by the formula given as
Shunt, S=i−igRAig
Substituting the value of ammeter resistance and the current values in the above equation
S=5−1.00.8×1.0=0.2Ω
Therefore the value of the shunt resistance must be 0.2 ohm
ii) Now the combined resistance of the ammeter and the shunt wire is given as
Rtotal1=RA1+S1
Substituting the values of the ammeter resistance and the shunt resistance in the above equation
\dfrac{1}{{{R_{total}}}} = \dfrac{1}{{0.8}} + \dfrac{1}{{0.2}} \\\
{R_{total}} = \dfrac{{0.8}}{5} \\\
{R_{total}} = 0.16\Omega \\\
Therefore the total resistance of the combined ammeter resistance and the shunt wire resistance is 0.16 ohm.
Note- The resistance of the shunt remains constant with time. The temperature coefficient of the instrument and the shunt remains low and same. The temperature coefficient shows the relation between the variations in the physical properties of the apparatus concerning the change in the temperature.
