Question

An ammeter and a voltmeter are joined in series to a cell. Their readings are A and V respectively. A resistance is now joined in parallel with the voltmeter. Then,
A.Both A and V will increase
B.Both A and V will decrease
C.A will decrease, V will increase
D.A will increase, V will decrease

Answer 1

Remember that when a resistance is joined in parallel, the effective resistance across the circuit decreases. To this end, using Ohm’s law determines how the V and A would change.
Formula Used:
Ohm’s law for voltage drop $V =IR$, where I is the current flowing through the resistor and R is the resistance offered by the resistor.
The net resistance for two resistors $R_1$ and $R_2$ connected in parallel: $R_{net} = \dfrac{R_1 R_2}{R_1 +R_2}$

Complete answer:
Let us begin by understanding what an ammeter and a voltmeter is.
An ammeter is a device that is used to measure the electric current in a circuit whereas a voltmeter is used to measure the voltage across two points in a circuit.
Generally, the internal resistance of the ammeter $R_A$ is low. To effectively measure the current passing through the circuit, the drop in voltage has to be as little as possible, which means that it should be able to have the current pass through it with a minimum or a low resistance.
The internal resistance of a voltmeter $R_V$ however, is generally high, so that it may not change the amount of current passing through it by drawing current and measures the voltage efficiently.
Thus, the ammeter has low resistance whereas the voltmeter has a high resistance to prevent loading effect, which is when a measuring instrument begins to act like a load and draws voltage or current from the circuit.
Now, getting back to our question,
Initial circuit:

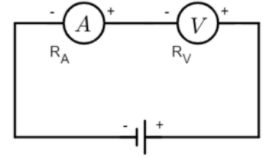
The net resistance in the initial circuit will be $R_{net} = R_A +R_V$
And from Ohm’s law in the context of the question: $R_{net} = \dfrac{V}{A}$, where V is the voltage and A is the current as recorded by the voltmeter and the ammeter respectively.
Final circuit:
Now, when a resistance $R_P$ is joined in parallel to the voltmeter, it forms an additional path for the current to pass through.

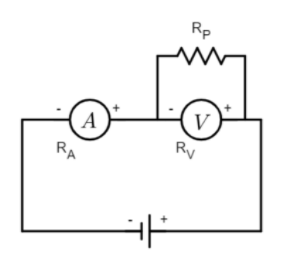
The net resistance is mathematically given as:
$R_{net} = R_A + \dfrac{R_P R_V}{R_P +R_V}$, which is evidently always less than $R_{net}$ of the initial case.
This means that the effective resistance of the entire circuit will reduce.
From Ohm’s law for this circuit
$R _{net}= \dfrac{V}{A}$ where V and A are voltmeter readings and ammeter readings for the final circuit now.
Since there is a decrease in the effective resistance, from the above relation, we can deduce that since $R_{net} \propto V$, there will be a decrease in V,
and since $R_{net} \propto \dfrac{1}{A}$, a decrease in $R_{net}$ will cause an increase in A.

Therefore, the correct choice would be C. A will increase, V will decrease.

Note:
Remember that when a circuit is connected in series, the current flowing through all circuit components will be the same and the voltage drop across each component may be different, whereas, in a parallel circuit, the voltage across the different branches of the circuit will be the same while the current flowing through the branches gets distributed, with the branch of least resistance getting maximum current flow.
This is also the same reason why the voltmeter might read a lower voltage if a resistance is connected in parallel to it. This is because the internal resistance of the voltmeter, like we discussed, is generally very high and if a relatively low resistance in introduced in a parallel branch, most of the current gets diverted to the path of least resistance and the voltmeter receives relatively lesser current and is thus able to process it and show a lesser voltage.
And since a large part of the current passes through the least resistance (across which there is a lesser drop in voltage), a relatively larger current is read by the ammeter than when it received current through the voltmeter.