Solveeit Logo
Login

Question

Question: An alternating voltage \(e = 200\sqrt2 sin(100t)\) volts is connected to \(1\mu F\) capacitor throug...

An alternating voltage e=2002sin(100t)e = 200\sqrt2 sin(100t) volts is connected to 1μF1\mu F capacitor through AC ammeter.The reading of the ammeter is:

A.5mA B.10mA C.15mA D.20mA \begin{aligned} & A.5mA \\\ & B.10mA \\\ & C.15mA \\\ & D.20mA \\\ \end{aligned}

Explanation

Solution

Hint: Take the impedance of the capacitor as Zc=1jωCZ_c = \dfrac{1}{j\omega C} and calculate the current in the circuit using ohm's law and phasors and then find the RMS value of the current.

Step by step solution:
The given circuit can be drawn as

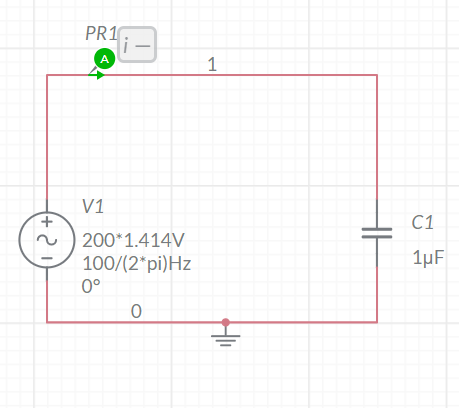
The given voltage source is Vs=2002sin(100t)=2002∠0oV_s = 200\sqrt2 sin(100t) = 200\sqrt2 \angle 0^o
Where 2002∠0o200\sqrt2 \angle 0^o is the phasor representation of the voltage

The capacitance given is: 1μF1\mu F

So the impedance of the capacitor is Zc=1jωC=−j100×10−6=104∠−90oZ_c = \dfrac{1}{j \omega C} = \dfrac{-j}{100 \times 10^{-6}} = 10^{4}\angle -90^o

We also know that ohm's law is given by I=VRI = \dfrac{V}{R}

Where V is the voltage across impedance and I is the current through the impedance.
The current in a circuit according to ohm's law becomes…

I=2002∠0o104∠−90o=22×10−2∠90o==22×10−2sin(100t+∠90o)=22×10−2cos(100t)I = \dfrac{200\sqrt2 \angle 0^o}{10^{4}\angle -90^o} = 2\sqrt2 \times 10^{-2} \angle 90^o = = 2\sqrt2 \times 10^{-2}sin(100t + \angle 90^o) = 2\sqrt2 \times 10^{-2}cos(100t)

Now we know the Ammeter always shows the RMS value of current.

So we know the RMS value of sinusoidal current of peak value IoI_o is given by Io2\dfrac{I_o}{\sqrt2}

So the RMS value of the current in the circuit is 20×10−3=20mA20\times 10^{-3} = 20 mA
So, we have used the phasor representation of impedance and voltage and calculated the current and its RMS value. Thus, we got the required ammeter reading as 20 mA.

Note: The easiest way of solving questions related to capacitor and inductor is by taking the values in the phasor representation. One of the possible mistakes that can be done in this kind of problems is that if we take the peak value of the sinusoidal current as the ammeter reading the ammeter always shows us the RMS value or the effective DC value of the sinusoidal current so so we need to take the RMS value of the current when ammeter reading is asked.