Question

An airplane is flying in the geographic meridian vertical plane at an angle ${30^ \circ }$ above with the horizontal (north) and the wind is blowing from the west. A package is dropped from an airplane. The velocity of the wind if a package hits a kite flying in space with a position vector R=($400\sqrt 3 i + 80j + 200k$) m with respect to the point of dropping. (Here i and j are unit vectors along north and vertically up respectively and k be the unit vector due east).

Answer 1

To solve this question draw the graphs with the unit vectors and then write the velocity of the airplane and wind in terms of the unit vector. After this, derive the velocity of the package and convert it into distance using the equation, distance is equal to speed multiplied by time. After this equates the derived package distance to the position vector mentioned in the question. After comparing and simplifying the equations the speed of the wind can be found.
Formula used: $S = ut - \dfrac{1}{2}g{t^2}$

Complete step-by-step solution:

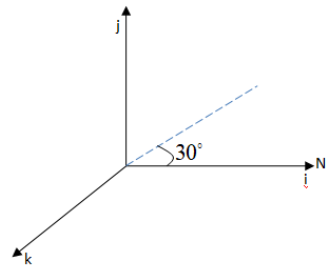
The airplane is flying at an angle ${30^ \circ }$ in the geographic meridian vertical plane.
From the above graph, we can write the velocity of the plane as,
In the $x$ direction the component is given by $u\cos {30^ \circ }$and the $y$ direction the component is given by $u\sin {30^ \circ }$
Therefore we get, ${V_p} = u\cos {30^ \circ }i + u\sin {30^ \circ }j$
Velocity of the wind $V_w = V k$
The distance of the package falling downwards in the j direction can be given using the equation,
${S_j} = {u_j}t - \dfrac{1}{2}g{t^2}$
Since the package is falling along the y axis ${u_j} = u\sin {30^ \circ }$
${S_j} = u\sin {30^ \circ }t - \dfrac{1}{2}g{t^2}$
Substituting the value of gas 10
We get, ${S_j} = u\sin {30^ \circ }t - \dfrac{1}{2} \times 10 \times {t^2}$
${S_j} = \dfrac{{ut}}{2} - 5{t^2}$…….. (1)
The velocity of the package is given by ${V_{package}} = u\cos {30^ \circ }i + u\sin {30^ \circ }j + vk$
Distance=speed$\times$time
Therefore we get,
$S = ut\cos {30^ \circ }i + ut\sin {30^ \circ }j + vtk$ …………… (2)
${S_j} = u\sin {30^ \circ }$……… (3)
Substitute equation (1) and equation (3) in equation (2) We get,
$S = ut\cos {30^ \circ }i + ut\sin {30^ \circ }j + vtk$
$S = ut\cos {30^ \circ }i + \left(\dfrac{{ut}}{2} - 5{t^2}\right)j + vtk$
Substitute the value of $\cos {30^ \circ }$ in the above equation
We get, $S = ut\dfrac{{\sqrt 3 }}{2}i + \left(\dfrac{{ut}}{2} - 5{t^2}\right)j + vtk$…………. (4)
Equating the given position vector of the package $R = 400\sqrt 3 i + 80j + 200k$ and equation (4)
We get, $400\sqrt 3 i + 80j + 200k$ $= ut\dfrac{{\sqrt 3 }}{2}i + \left(\dfrac{{ut}}{2} - 5{t^2}\right)j + vtk$
Comparing the equations we get
$\Rightarrow 400\sqrt 3 = ut\dfrac{{\sqrt 3 }}{2}$………… (5)
$\Rightarrow 80 = \dfrac{{ut}}{2} - 5{t^2}$ …………. (6)
$\Rightarrow vt = 200$ ……………. (7)
Therefore by simplifying equation (5) we get, $400\sqrt 3 = ut\dfrac{{\sqrt 3 }}{2};400 = \dfrac{{ut}}{2};ut = 800$
Substituting the value of ut in equation (6) we get,
$80 = \dfrac{{ut}}{2} - 5{t^2}$
$\Rightarrow 80 = \dfrac{{800}}{2} - 5{t^2}$
$\Rightarrow 80 = 400 - 5{t^2}$
Rearranging the equation, $320 = 5{t^2}$
Therefore we get ${t^2} = \dfrac{{320}}{5} = 64$
Taking the square root $t\; = 8$
Substitute the value of t in equation (7)
$vt = 200$
$\Rightarrow v = \dfrac{{200}}{8} = 25$
Therefore we get the speed of the wind to be $25m{s^{ - 1}}$

Note: While solving the questions of this type the velocity of the object should be written in the component form. If the question contains numbers in Km/h and if it is necessary to convert it into m/s we just have to multiply the value given in Km/h by $\dfrac{5}{{18}}$ to get the value in m/s.