Question
Question: An airplane is flying in a horizontal direction with a velocity 600 km/hr at a height of 1960 m. Whe...
An airplane is flying in a horizontal direction with a velocity 600 km/hr at a height of 1960 m. When it is vertically above the point A on the ground, a body is dropped from it. The body strikes the ground at point B. Calculate the distance AB.
Solution
Use kinematic equation in the vertical direction of the motion of the body to determine the time taken by the body to reach the point B. Initially, the body has only horizontal components of initial velocity. Use the kinematic equation in the horizontal direction to determine the distance AB.
Formula used:
s=ut+21at2
Here, s is the distance, u is the initial velocity, a is the acceleration and t is the time.
Complete step by step answer:
We can picture the fall of the body from the plane as shown in the figure below.
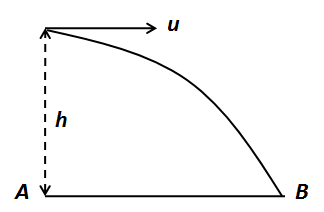
We can determine the horizontal distance AB, if we know the time taken by the body to reach point B from the airplane.
We can calculate the time using kinematic equation in vertical direction as follows,
h=uyt+21gt2
Here, uy is the vertical component of initial velocity, h is the vertical distance covered by the body, g is the acceleration due to gravity and t is the time.
We know that for when the body dropped from the airplane, it has only horizontal motion of the airplane. Therefore, we can substitute 0 for uy in the above equation.
h=21gt2
⇒t=g2h
Substitute 1960 m for h and 9.8m/s2 for g in the above equation.
t=9.82(1960)
⇒t=400
⇒t=20s
Now, we can use kinematic equation in horizontal direction of the body as follows,
sAB=uxt
Here, ux is the horizontal component of initial velocity of the body.
We substitute 600 km/hr for ux and 20 s for t in the above equation.
sAB=((600hrkm)(1km1000m)(3600s1hr))(20s)
⇒sAB=3333m
⇒sAB=3.33km
Therefore, the horizontal distance AB is 3.33 km.
Note:
Almost every question relating velocity, distance and acceleration can be solved using kinematic equations. Students should learn how to use the kinematic relations in vertical and horizontal direction. One term in the kinematic equation can be eliminated by using it in horizontal or vertical direction just like we eliminated the term of vertical component of initial velocity to determine the time of flight. Note that, the acceleration due to gravity does not affect the horizontal motion of the body.
