Solveeit Logo
Login

Question

Question: An aircraft moving with a speed of \(250\,m{s^{ - 1}}\)at a height of, overhead by anti aircraft-gun...

An aircraft moving with a speed of 250 ms−1250\,m{s^{ - 1}}at a height of, overhead by anti aircraft-gun. If the muzzle velocity is 500 ms−1500\,m{s^{ - 1}}, the firing angle θ\theta should be:
A. 30∘{30^ \circ }
B. 60∘{60^ \circ }
C. 45∘{45^ \circ }
D. 75∘{75^ \circ }

Explanation

Solution

From the given question we have to find out the angle at a certain point for this type of calculation we are going to use the given data and trigonometry formulas. Before going into the solution part once check the given values.

Complete step by step answer:
When an aircraft is moving with a speed of 250 ms−1250\,m{s^{ - 1}}at a height of 6000 m6000\,m. From ground we are hiring an anti aircraft-gun with speed 500 ms−1500\,m{s^{ - 1}}with an angle θ\theta .

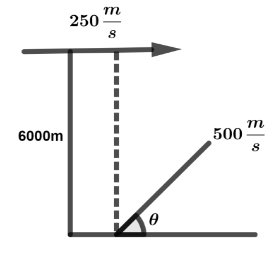
Now we are assuming the horizontal component and vertical component, whereas horizontal component is 500cos⁡θ500\cos \theta and vertical component is 500sin⁡θ500\sin \theta .
For overhead an anti aircraft gun u(x)=250ms−1→(1)u\left( x \right) = 250m{s^{ - 1}} \to \left( 1 \right)
Given that u(x)=500cos⁡θu\left( x \right) = 500\cos \theta
Substitute the value of u(x)u\left( x \right)in equation (1), then we get
500\cos \theta = 250 \\\ \Rightarrow \cos \theta = \dfrac{{250}}{{500}} \\\ \Rightarrow \cos \theta = \dfrac{1}{2} \\\ \Rightarrow \theta = {\cos ^{ - 1}}\dfrac{1}{2} \\\
From trigonometry formulas we know the values of cos⁡−1θ{\cos ^{ - 1}}\theta where as cos⁡−112{\cos ^{ - 1}}\dfrac{1}{2} that means the θ\theta value is, θ=60∘\theta = {60^ \circ }.

Hence, the correct option is B.

Additional information:
If an object changes its direction or position with respect to frame of reference and function of time is called Velocity. Velocity units are measured distance by time. The velocity of a projectile when it leaves the influence of a muzzle. Now day modern velocities are taken by the chronographers, but as per history it was not possible.

Note: When the bullet passes from the gun then the timer begins and when the bullet passes through the second laser then the timer stops. In this question we are using an empty aircraft gun only to measure the firing angle. But in other cases we can use aircraft guns and anti aircraft guns.