Question

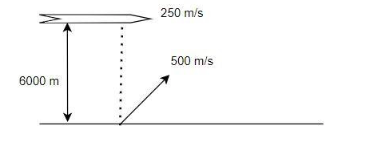
An aircraft moving with a speed of $250\,m{s^{ - 1}}$ is at a height of $6000\,m$, just overhead of an anti-aircraft- gun. If the muzzle velocity is $500\,m{s^{ - 1}}$ , the firing angle $\theta$ should be:

(A) ${30^ \circ }$
(B) ${45^ \circ }$
(C) ${60^ \circ }$
(D) ${75^ \circ }$

Answer 1

Observe the given diagram and split the velocity of the muzzle into the horizontal component and the vertical component. Equate the horizontal component of the velocity of the muzzle to the velocity of the aircraft, to find out the firing angle of the gun.

Complete step by step solution:
Given,

Speed of the aircraft, $V = 250\,m{s^{ - 1}}$

The speed of the muzzle, $v = 500\,m{s^{ - 1}}$

The aircraft flies at the height, $h = 6000\,m$

The muzzle velocity is inclined to a certain angle, so that it can fire the aircraft. So this inclined velocity is separated into the vertical component as $500\sin \theta$ and the horizontal component as $500\cos \theta$ . This separation of the horizontal and the vertical component helps us to calculate the angle of the inclination of the gun to fire the aircraft.

Since the horizontal component of the gun and the aircraft are straight to each other and moves in the similar direction,

$500\cos \theta = 250$

By grouping the similar terms in both sides of the equation, we get

$\cos \theta = \dfrac{1}{2}$

In order to find the angle of the inclination, the cos is taken as the inverse in the right hand side of the equation,

$\theta = {\cos ^{ - 1}}\left( {\dfrac{1}{2}} \right) = {60^ \circ }$

Thus the firing angle ${60^ \circ }$ is needed to fight the aircraft with the help of the muzzle.

Thus the option (C) is correct.

Note: While separating the components of the velocity, the $\sin \theta$ is taken as the vertical component and the $\cos \theta$ is considered as the horizontal component. This is because the horizontal component must have a larger value, since the least value of the $\cos$ is $1$ and it still increases further. But $\sin \theta$ values range from $0\,to\,1$ .