Question: An aircraft is flying at a height of 3400 m above the ground. If the angle subtended at a ground obs...

Question

An aircraft is flying at a height of 3400 m above the ground. If the angle subtended at a ground observation point by the aircraft positions 10.0s apart is 30°, what is the speed of the aircraft?

Answer 1

Solution

Hint: Draw the diagram of the system. Use the simple trigonometric equations to find the distance travelled by the aircraft in the given time. Now, divide the distance travelled by the time of flight to determine the speed of the aircraft.

Formula Used:
We have used the normal trigonometric definition of tanθ

$\tan \theta =\dfrac{height}{base}$

Speed of a particle is given by,

$s=\dfrac{d}{t}$
Where, s is the speed of the particle,
d is the distance travelled,
and t is the time taken to travel the distance.

Complete step by step solution:
First, let’s draw the system as mentioned in the question. The following diagram shows the path of the aircraft and location of the observatory.

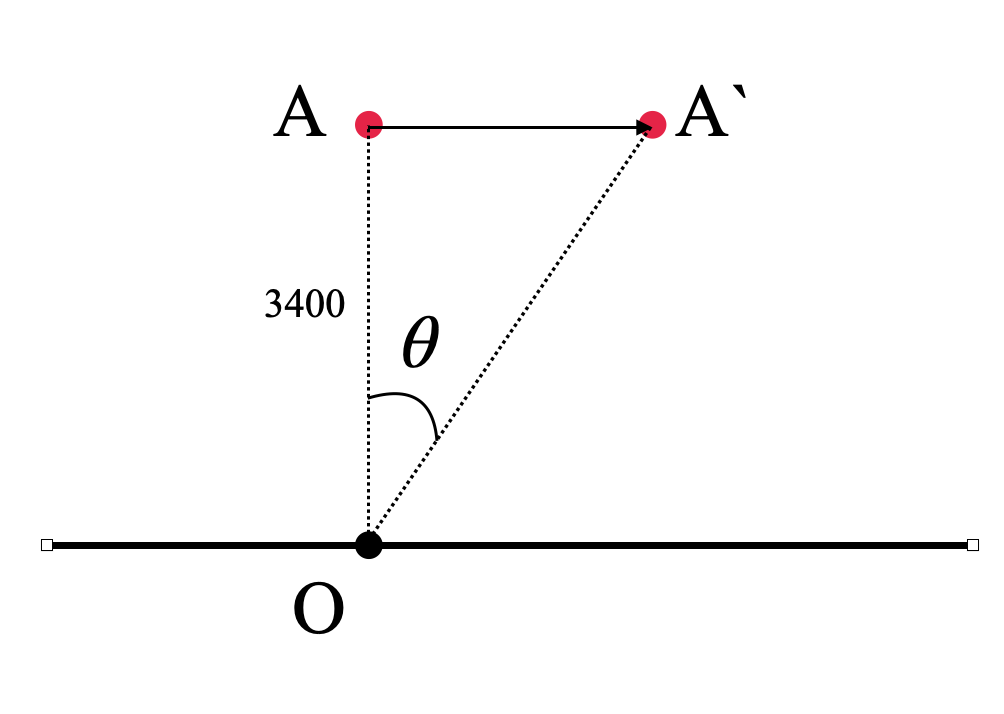
As we can see, the airplane has travelled a distance of AA in the 10s. So, we can find the speed of the airplane if we can find the distance AA.
The height of the airplane’s path is 3400m.

Hence the value of, OA is 3400m.
We know the angle AOA`, which is 30°.

We can simply use the tangent formula to determine the length of AA. In the triangle OAA, using equation 1, we can say that,

$\tan {{30}^{0}}=\dfrac{AA\grave{\ }}{OA}$
$\Rightarrow AA\grave{\ }=OA\times \tan {{30}^{0}}$
$\Rightarrow AA\grave{\ }=3400\times \tan {{30}^{0}}$
$\Rightarrow AA\grave{\ }=1963$
Hence, the length of AA` is, 1963 m.

We can use equation (2) to determine the speed of the airplane.
Now, the speed of the airplane is given by,
$s=\dfrac{AA\grave{\ }}{t}$
$\Rightarrow s=\dfrac{1963}{10}$
$\Rightarrow s=196.3$
Hence the final answer is, 196.3 m/s

Note:
We can assume that the airplane is moving parallel to the ground. Otherwise, we had to take the direction of the airplane into consideration as well. The most common mistake for this kind of question is the absence of diagrams. For a geometrical problem like this, you need to visualize the problem. This will help you in determining the values easily, and you will avoid any unnecessary calculation mistakes.