Solveeit Logo
Login

Question

Question: An aircraft executes a horizontal loop of radius 1.00 km with a steady speed of 900 km/h. Compare it...

An aircraft executes a horizontal loop of radius 1.00 km with a steady speed of 900 km/h. Compare its centripetal acceleration with the acceleration due to gravity.

Explanation

Solution

Hint: To maintain circular motion of aircraft, we need centripetal acceleration. Use the formula of centripetal acceleration and we know the value of acceleration 9.8m/s29.8m/{{s}^{2}}. To compare centripetal acceleration with the acceleration due to gravity, take ratio of both the quantities.

Complete step by step solution:

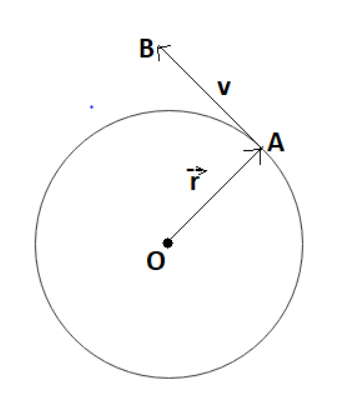
where,
OA= radius of circular loop
AB= tangential drawn to the radius vector
O is the center

We have given that the radius of the circular path is 1 km1\text{ }km. Speed of aircraft is 900km/s900km/s.
Centripetal acceleration is the acceleration which acts on a particle performing circular motion, which is a long radius of circle and directed towards the center of the circle.
Mathematically, centripetal acceleration is expressed as,
ac=−v2r{{a}_{c}}=-\dfrac{{{v}^{2}}}{r}
Since we are considering only magnitude since we have given speed, not velocity. Therefore take mode of centripetal force and we get,
ac=v2r{{a}_{c}}=\dfrac{{{v}^{2}}}{r}
Where,
v= speed of aircraft
r= radius of loop
ac{a}_{c}= acceleration due to gravity

Convert speed of aircraft in M.K.S system.

& \text{Speed of the aircraft, v=900km/h=900 }\\!\\!\times\\!\\!\text{ }\dfrac{\text{5}}{\text{18}}\text{=250m/s} \\\ & v=250m/s \\\ \end{aligned}$$ $$r=\text{ }1km=1000m$$ ${{a}_{c}}=\dfrac{{{v}^{2}}}{r}=\dfrac{{{\left( 250 \right)}^{2}}}{1000}=62.5m/{{s}^{2}}$ Now we know that acceleration due to gravity is given as $g=9.8m/{{s}^{2}}$ To compare take ratio acceleration due to gravity and centripetal force. We get, $\begin{aligned} & \dfrac{{{a}_{c}}}{g}=\dfrac{62.5}{9.8}=6.38 \\\ & {{a}_{c}}=6.38g \\\ \end{aligned}$ Note: Students should know that to perform circular motion, centripetal force is necessary. To balance this force (so that aircraft shouldn’t fall down and maintain circular path) there must be another force which is known as centrifugal force. Centrifugal force directed radially away from the center of the circle. Because of this force only aircraft is maintaining circular motion.