Question

An air chamber of volume V has a neck of cross sectional area into which a light ball of mass m and can move up and down without friction. The diameter of the ball is equal to that of the neck of the chamber. The ball is pressed down a little and released. If the bulk modulus for air is B, the time period of the oscillation of the ball is
$\begin{aligned} & a)T=2\pi \sqrt{\dfrac{B{{a}^{2}}}{mV}} \\\ & b)T=2\pi \sqrt{\dfrac{BV}{m{{a}^{2}}}} \\\ & c)T=2\pi \sqrt{\dfrac{mB}{V{{a}^{2}}}} \\\ & d)T=2\pi \sqrt{\dfrac{mV}{B{{a}^{2}}}} \\\ \end{aligned}$

Answer 1

It is given in the question that the ball has the same diameter as compared to the neck of the chamber. Hence there will be no escape of air from the container to the surrounding. When we press the light ball of mass m towards the inner side along the neck, the pressure in the chamber will increase and will tend to attain the equilibrium position. As a result the ball will be pushed by the force of air inside. There will be a point where the pressure outside i.e. atmospheric pressure will be greater than the pressure inside, a result of which the ball will again move down. This process will keep on continuing till the energy is lost by the ball. Hence the ball will perform S.H.M. We will use the expression of the bulk modulus and the equation of time period of S.H.M to determine the time period of the ball.

Formula used:
$B=\dfrac{\text{Pressure}}{\text{Volume strain}}=\dfrac{P}{-\Delta V/V}$
$T=2\pi \sqrt{\dfrac{m}{k}}$

Complete step by step answer:

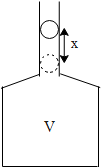
In the above figure we can see that the ball of mass ‘m’ is pushed inside the chamber along the neck of the cross sectional area ‘a’, by distance ‘x’ from its position of equilibrium. The bulk modulus for air when there is a strain in the volume (V) for a particular pressure( P) is given by,
$B=\dfrac{\text{Pressure}}{\text{Volume strain}}=\dfrac{P}{-\Delta V/V}$
Where $\Delta V=a\text{x}$ is the change in the volume.
This increase in pressure will exert a restoring force on the ball. Since force $F(restoring)$ acting along the neck is equal to pressure times area of the cross sectional of the neck of the chamber, the above equation can be written as,
$\begin{aligned} & B=\dfrac{F(restoring)}{a\left( -\Delta V/V \right)} \\\ & \Rightarrow F(restoring)=-\dfrac{B\times a\Delta V}{V},\text{since }\Delta \text{V=ax} \\\ & \Rightarrow F(restoring)=-\dfrac{B\times a\left( ax \right)}{V} \\\ & \Rightarrow F(restoring)=-\dfrac{B\times {{a}^{2}}x}{V} \\\ \end{aligned}$
When a spring is stretched due to the mass m attached to it by a distance y, the restoring force is given by $F=-ky....(2)$ where k is the spring constant. If the spring is stretched and left, it will perform S.H.M whose time period is given by,
$\begin{aligned} & T=2\pi \sqrt{\dfrac{\text{Inertial mass}}{\text{spring constant}}} \\\ & \Rightarrow T=2\pi \sqrt{\dfrac{m}{k}}.....(3) \\\ \end{aligned}$
If we compare equation 1 and 2, the restoring force on the ball of mass m varies with a constant i.e. $\dfrac{B{{a}^{2}}}{V}$ times the compression produced along the neck of the air. Hence we can say that the factor k of the spring is equivalent to $\dfrac{B{{a}^{2}}}{V}$ of the S.H.M of the ball. Therefore using equation 3 the time period of oscillation of the ball of mass m is equal to,
$\begin{aligned} & T=2\pi \sqrt{\dfrac{m}{k}} \\\ & \Rightarrow T=2\pi \sqrt{\dfrac{m}{\dfrac{B{{a}^{2}}}{V}}} \\\ & \Rightarrow T=2\pi \sqrt{\dfrac{mV}{B{{a}^{2}}}} \\\ \end{aligned}$

So, the correct answer is “Option D”.

Note:
The above equation is valid only if the pressure and the volume is varied isothermally. This is because if the temperature is not constant then the pressure and the volume will change by itself and the time period observed might not be a constant. It is also to be noted that the pressure inside the chamber should be greater than the atmospheric pressure when the ball is pushed downwards.