Question

An aeroplane when flying at a height of $3125m$ from the ground passes vertically below another plane at an instant when the angles of elevation of the two planes from the same point on the ground are $30^\circ$ and $60^\circ$ respectively. Find the distance between the two planes at the instant.

Answer 1

Hint : Here, we will draw the diagram with the given specifications and with the help of trigonometric functions and the given angle we will find the unknown distance.

Complete step-by-step answer :

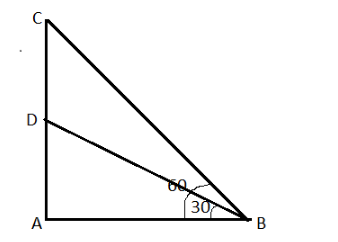
Let AB the surface of the ground, at point B there is the observer which finds two aeroplanes at point D and C with the angle of elevation of $30^\circ {\text{ and 60}}^\circ$ .
We are given distance of one plane with the ground, $AD = 3125m$
We have to find the distance between two planes, $CD$
In $\Delta DAB,$
Tangent function is opposite upon the adjacent side.
$\Rightarrow \tan 30^\circ = \dfrac{{AD}}{{AB}}$
Place the known values in the above equations,
$\dfrac{1}{{\sqrt 3 }} = \dfrac{{3125}}{{AB}}$
Do-cross multiplication
$\Rightarrow AB = 3125\sqrt 3 m$ ..... (a)
In $\Delta CBA$ ,
$\tan 60^\circ = \dfrac{{AD + DC}}{{AB}}$
Place the known values in the above equations –
$\sqrt 3 = \dfrac{{3125 + DC}}{{AB}}$
Do-cross multiplication and make AB the subject –
$AB = \dfrac{{3125 + DC}}{{\sqrt 3 }}{\text{ }}$ .... (b)
From the equations (a) and (b), we can equate each of the equation’s right hand side of the equation
$3125\sqrt 3 = \dfrac{{3125 + DC}}{{\sqrt 3 }}{\text{ }}$
Do-cross multiplication and simplify
$3125\sqrt 3 \times \sqrt 3 = 3125 + DC$
Apply the property of the product of two same square-roots given the number.
$3125 \times 3 = 3125 + DC \\\ 9375 = 3125 + DC \\\$
When any term changes its sides, the sign also changes. Positive becomes negative and negative becomes positive.
$\Rightarrow DC = 9375 - 3125 \\\ \Rightarrow DC = 6250m \\\$
Hence, the distance between the two planes is $6250m.$

Note : Remember the basic difference between the angles of the elevation and the depression and apply accordingly. And remember the basic trigonometric functions and its values for direct substitution of its correct value.