Solveeit Logo
Login

Question

Question: An aeroplane when flying at a height of 2000 m from the ground passes vertically above helicopter at...

An aeroplane when flying at a height of 2000 m from the ground passes vertically above helicopter at an instant when the angles of the elevation of the two planes from the same point on the ground are 60∘{{60}^{\circ }} and 30∘{{30}^{\circ }} respectively. Find the vertical distance between the helicopter from the ground.

Explanation

Solution

Hint: We will be using the concept of trigonometry to solve the problem we will also be using concept of height and distances to further simplifying the problem
We will first draw a diagram to understand the question

Complete step-by-step answer:

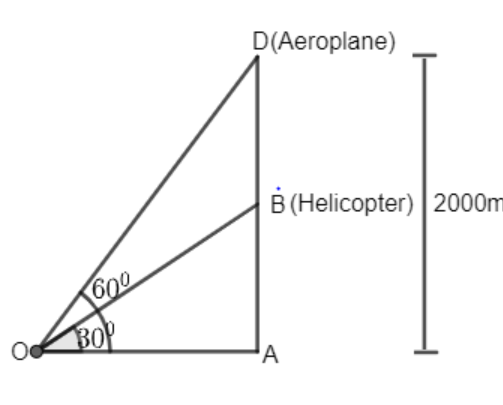
We have given that the elevation of both aeroplane and helicopter is 60∘{{60}^{\circ }} and 30∘{{30}^{\circ }} respectively
Now we have to find the vertical height of helicopter from ground i.e. AB
We have been given the vertical height of aeroplane from ground i.e. AD = 2000
We will first find the value of base OA through trigonometry in ΔOAD\Delta OAD
So, we have ΔOAD\Delta OAD now we will apply,
tan⁡60∘=PerpendicularBase ⇒3=ADOA ⇒3=2000OA OA=20003m...........(i) \begin{aligned} & \tan {{60}^{\circ }}=\dfrac{Perpendicular}{Base} \\\ & \Rightarrow \sqrt{3}=\dfrac{AD}{OA} \\\ & \Rightarrow \sqrt{3}=\dfrac{2000}{OA} \\\ & OA=\dfrac{2000}{\sqrt{3}}m...........(i) \\\ \end{aligned}
Now we will apply trigonometry in ΔOBA\Delta OBA
So, we have
tan⁡30∘=ABOA 13×OA=AB \begin{aligned} & \tan {{30}^{\circ }}=\dfrac{AB}{OA} \\\ & \dfrac{1}{\sqrt{3}}\times OA=AB \\\ \end{aligned}
We will substitute OA from (i)
13×20003=AB 20003m=AB \begin{aligned} & \dfrac{1}{\sqrt{3}}\times \dfrac{2000}{\sqrt{3}}=AB \\\ & \dfrac{2000}{3}m=AB \\\ \end{aligned}
So, the vertical distance between helicopter and ground is 20003m\dfrac{2000}{3}m

Note: To solve these types of questions it is important to note that we have first applied trigonometric ratios in upper triangle DOA to find the base OA then we have applied trigonometry ratio in the smaller triangle BOA to find the height of the helicopter. It is also helpful to remember trigonometric relations like,
tan⁡θ=PB cos⁡θ=BH sin⁡θ=PH \begin{aligned} & \tan \theta =\dfrac{P}{B} \\\ & \cos \theta =\dfrac{B}{H} \\\ & \sin \theta =\dfrac{P}{H} \\\ \end{aligned}