Question

An Aeroplane is in a level flight at 144km/hr at an altitude of 1000m. How far from a given target is a bomb to be released from it to hit the target?
A. 566m
B. 671.43m
C. 471.34m
D. 371.34m

Answer 1

We will first calculate the time bomb will take to hit the target by using the equation of kinematics. Then, we will substitute this time value in the distance formula and then we get the required answer.
Formula:
$h={{u}_{y}}+\dfrac{1}{2}{{a}_{y}}{{t}^{2}}$
$x={{v}_{x}}\times t$

Complete answer:
In the question the speed of the aeroplane is given in km/hr and altitude in meters. So, we will start by converting speed in m/s.
$\begin{aligned} & {{v}_{x}}=144\times \dfrac{5}{18}m/s \\\ & \therefore {{v}_{x}}=40m/s\text{ -----(1)} \\\ \end{aligned}$

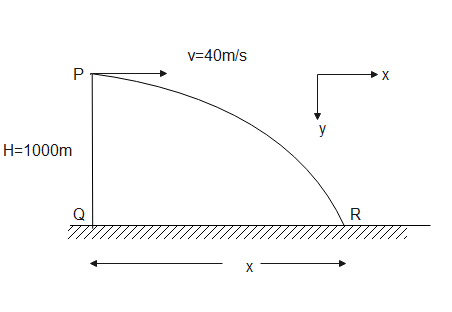
Now, we can write the horizontal distance
$x={{v}_{x}}\times t\text{ ----(2)}$
Where v is the velocity of the aeroplane and t is the time.
As the plane is moving in a horizontal direction, the component of velocity in the vertical direction will be zero. That is ${{v}_{y}}=0$. Same is applicable to the bomb it is dropped from the plane.
We will now consider the vertical motion of the bomb to find the time it will take to hit the target. So, acceleration due to gravity will act on the bomb such that ${{a}_{y}}=10m/{{s}^{2}}$. The bomb will be dropped with a height of 1000m i.e h=1000m.
Using the kinematic equation

& h={{u}_{y}}+\dfrac{1}{2}{{a}_{y}}{{t}^{2}} \\\ & \Rightarrow h=\dfrac{1}{2}g{{t}^{2}} \\\ & \Rightarrow t=\sqrt{\dfrac{2h}{g}} \\\ & \Rightarrow t=\sqrt{\dfrac{2\times 1000}{10}} \\\ & \Rightarrow t=\sqrt{200} \\\ & \Rightarrow t=14.14s \\\ \end{aligned}$$ Now , we will substitute this value in equation (2), we get $\begin{aligned} & \Rightarrow x=40\times 14.14 \\\ & \Rightarrow x=565.68m \\\ & \therefore x\cong 566m \\\ \end{aligned}$ So, the bomb must be released from 566m away so that it hits the target. **Hence, Option(A) is correct.** **Note:** One must remember that while converting speed in km/hr to speed in m/s we have to multiply speed in km/hr by a factor of $\dfrac{5}{18}$. If we need to convert speed in m/s to speed in km/hr we multiply speed by a factor of $\dfrac{18}{5}$. When an object falls from a certain height only it will fall with acceleration due to gravity g, because only gravitational force acts on it ideally.