Question

An aeroplane is flying horizontally at a height of 3150 m above a horizontal plane ground. At a particular instant it passes another plane vertically below it. At this instant, the angles of elevation of the planes from a point on the ground are $30^\circ$ and $60^\circ$ . Hence, the distance between the two planes at that instant is:
(A) 1050 m
(B) 2100 m
(C) 4200 m
(D) 5250 m

Answer 1

Hint : Let the required distance be $x$ . Draw a diagram using the given information to get two right angled triangles. Call the common base as $y$ . Use $\tan \theta = \dfrac{{Length{\text{ }}of{\text{ }}the{\text{ }}opposite{\text{ }}side}}{{Length{\text{ }}of{\text{ }}the{\text{ }}adjacent{\text{ }}side}}$ to get the equations $\tan 30^\circ = \dfrac{y}{{3150}} = \dfrac{1}{{\sqrt 3 }}$ and $\tan 30^\circ = \dfrac{{3150 - x}}{y} = \dfrac{1}{{\sqrt 3 }}$ . Solve them to get the answer.

Complete step-by-step answer :
We are given the information about the flight of a plane.
It is flying horizontally above a horizontal ground at a height of 3150 m.
It passes another aeroplane vertically below it at some point.
At this point, the angle of elevation for the lower plane is $30^\circ$ and the one flying above it is $60^\circ$ .
Call the distance between the two planes as $x$ .
Let’s draw a diagram using this information.
We can consider the height of the higher aeroplane from the ground as the perpendicular side of a right angled triangle.
Let the length of the base of the triangle be $y$ m. Then we get the following picture:

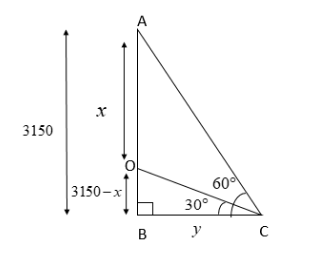
Thus, we get a right angled triangle ABC with perpendicular sides of length 3150 m and $y$ m; and another right angled triangle OBC with perpendicular sides of length $(3150 - x)$ m and $y$ m.
Also, the measures of the angles of both the triangles are $30^\circ ,60^\circ ,90^\circ$ .
We know that in a right angled triangle, $\tan \theta = \dfrac{{Length{\text{ }}of{\text{ }}the{\text{ }}opposite{\text{ }}side}}{{Length{\text{ }}of{\text{ }}the{\text{ }}adjacent{\text{ }}side}}$
In triangle ABC, $\tan 30^\circ = \dfrac{y}{{3150}} = \dfrac{1}{{\sqrt 3 }}$ .
This implies we have $y = \dfrac{{3150}}{{\sqrt 3 }}...(1)$
Similarly, in triangle OBC, $\tan 30^\circ = \dfrac{{3150 - x}}{y} = \dfrac{1}{{\sqrt 3 }}.....(2)$
Therefore using (1) in (2), we get
$\dfrac{{3150 - x}}{{\dfrac{{3150}}{{\sqrt 3 }}}} = \dfrac{1}{{\sqrt 3 }} \\\ \Rightarrow 3150 - x = \dfrac{1}{{\sqrt 3 }} \times \dfrac{{3150}}{{\sqrt 3 }} = \dfrac{{3150}}{3} \\\ \Rightarrow 3 \times (3150 - x) = 3150 \\\ \Rightarrow 9450 - 3x = 3150 \\\ \Rightarrow 3x = 9450 - 3150 = 6300 \\\ \Rightarrow x = 2100 \\\$
Hence, the distance between the two planes is 2100 m.

Note : Angles above the horizontal line are called angles of elevation. If a question contains these angles, then the diagrammatic representation of the word problem will give you a right angled triangle. This will give you the first approach for solving such problems.