Question

An aeroplane has to go from point A to another point B, $500\,km$ away due ${30^ \circ }$ east of north. A wind is blowing due north at a speed of $20\,m/s$. The air-speed of the plane is $150\,m/s$.
(a) Find the direction in which the pilot should head the plane to reach point B.
(b) Find the time taken by the plane to go from A to B.

Answer 1

Since velocity is a vector quantity a diagram using the concept of vectors in terms of the velocities is to be constructed. The equation using the law of sine of triangles is constructed in order to determine the direction of the aeroplane. The speed formula relating the distance and time is applied to get the time taken for the plane to go from point A to B.

Complete step by step answer:
The problem revolves around the concept of vectors which are used to indicate the direction in which the velocity quantity is in. The question says that an aeroplane has to fly from point A to point B.

(a) The velocity of the wind as well as the velocity of the plane while cutting through the air is given to be $20\,m/s$ and $150\,m/s$ respectively. The plane which was supposed to travel from point A to B has been deviated by an angle and hence this angle by which the path of the plane has been deviated or shifted by needs to be found out in order for the pilot to head the plane in the correct direction keeping the plane back on the path A to B.

The diagram below illustrates all of this data (where N indicates north direction and E indicates east direction):

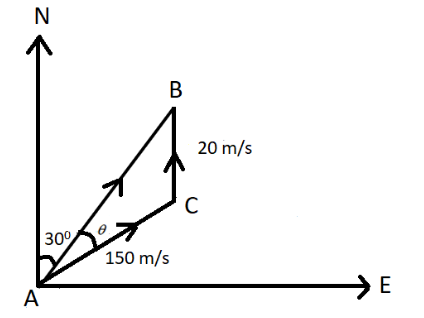
Here, the velocity of the wind that is blowing towards the north direction is given by the vector $\overrightarrow {CB}$ while its magnitude is $20m/s$. The velocity component that indicates the velocity of the plane with respect to the blowing wind is given by the vector $\overrightarrow {AC}$ and vector $\overrightarrow {AB}$ indicates the path of the plane, that is, the direction in which the plane must travel (from point A to B).

We can see that the angle subtended by the vector pointing in the north direction and the $\overrightarrow {AB}$ is ${30^ \circ }$. By the properties of triangles we know that by alternating angle property that the angle $\angle ABC$ is also ${30^ \circ }$ since alternating angles are said to be equal. This can be seen in the diagram below.

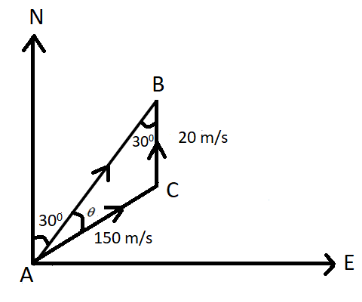
We now consider the triangle $\Delta ABC$ from the diagram above. Now, we can apply the law of sines or the sine rule in order to determine the unknown angle. The law of sines states that the ratios of their sides are equivalent to their corresponding sine angles. We assume the velocity vectors to be the sides of the triangle. Hence we get the equation:
$\dfrac{{20}}{{\sin \theta }} = \dfrac{{150}}{{\sin 30}}$

Hence by cross multiplying the terms of the above equation we get:
$20 \times \sin 30 = 150 \times \sin \theta$
$\Rightarrow 150 \times \sin \theta = 20 \times \dfrac{1}{2}$
$\Rightarrow 150 \times \sin \theta = 10$
$\Rightarrow \sin \theta = \dfrac{{10}}{{150}}$
$\Rightarrow \sin \theta = \dfrac{1}{{15}}$
$\Rightarrow \theta = {\sin ^{ - 1}}\dfrac{1}{{15}}$
$\therefore \theta \approx {3.8^ \circ }$

Hence the direction the pilot needs to head from east to north by an angle ${3.8^ \circ }$ to go from point A to B.

(b) In order to find the time taken we must apply the speed-distance formula. The distance from point A to B is given to be $500km$. We need to find the distance in meters because that is its SI unit.
Hence, we know that
$1\,km = 1000\,m$
$\Rightarrow 500\,km = 500 \times 1000$
$\Rightarrow 500\,km = 500000\,m$
The total angle that the plane needs to go in is given by:
$\Rightarrow {30^ \circ } + \theta$
$\Rightarrow {30^ \circ } + 3.8$
$\Rightarrow {33.8^ \circ }$
We now need to determine the speed or the velocity of the plane from point A to B. Let this unknown velocity be $x$. We now apply the cosine rule in order to find this unknown velocity.

The cosine rule for a triangle is applied to get:
${x^2} = {(AC)^2} + {(CB)^2} + 2 \times AC \times CB \times \cos \left( {33.8} \right)$
Taking square root on both the sides we get:
$\Rightarrow x = \sqrt {{{(AC)}^2} + {{(CB)}^2} + 2 \times AC \times CB \times \cos \left( {33.8} \right)}$
By substituting the velocity vector values we get:
$\Rightarrow x = \sqrt {{{(150)}^2} + {{(20)}^2} + 2 \times 150 \times 20 \times \cos \left( {33.8} \right)}$
By simplifying further we get:
$x = \sqrt {22500 + 400 + 6000 \times \cos \left( {33.8} \right)}$
$\Rightarrow x = \sqrt {27885.906}$
$\Rightarrow x = 166.99$
$\Rightarrow x \approx 167$
Hence the aeroplane travels with a velocity of approximately $167\,m/s$ from point A to B.

By the speed-distance formula we are aware that:
$\text{speed} = \dfrac{\text{distance}}{\text{time}}$
Hence by rearranging the terms we get:
$\text{time} = \dfrac{\text{distance}}{\text{speed}}$
Hence, we can find the time taken to travel from the point A to B by substituting the given values:
$\text{time} = \dfrac{{500000}}{{167}}$
$\Rightarrow \text{time} = 2994.011\,s$
We now convert time in seconds to minutes
We know that,
$1\min = 60\sec$
Hence by unitary method, $2994.011\sec = \dfrac{{2994.011}}{{60}}\min$
$\Rightarrow 49.90\min$
$\approx 50\min$

Hence the time taken to travel from A to B is $50\min$.

Note: An alternative way to solve the above problem is by breaking down the velocity vectors into their corresponding horizontal and vertical velocity components as there is an angle that is being formed. The velocity components that seem to be equal and opposite to each other are equated to get the direction to be taken by the pilot.