Question
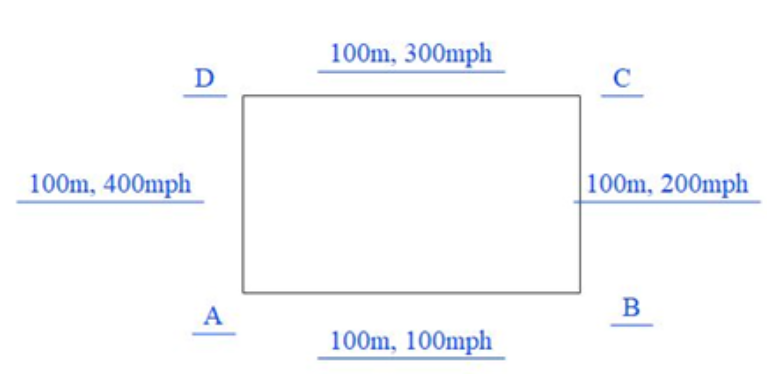
Question: An aeroplane covers around a square. It covers the four sides with speeds as 100, 200, 300, 400mph r...
An aeroplane covers around a square. It covers the four sides with speeds as 100, 200, 300, 400mph respectively. Find out the average speed of the aeroplane.
a)190b)195c)192d)200
Solution
As the sides of a square are equal, find the time taken to travel each side in terms of speed that is given in the question and time assumed. Next, we know the average speed is equal to the ratio between average distance and average time. The average time is the time taken to travel all the sides of the square.
Formulas used:
s=vt
Complete step-by-step solution:
Let the sides of the square be a, b, c, d respectively. Let us assume the time taken to travel the sides a to b, b to c, c to d and d to a as t1,t2,t3,t4respectively. Now, we can write the time taken in terms of distance and velocity as,
t1=100at2=200at3=300at4=400a
Total time taken can be found as,
T=t1+t2+t3+t4T=100a+200a+300a+400aT=120025a
Now, the total distance is 4aand the total time taken by the aeroplane is calculated above therefore, the average speed can be calculated as total distance divided by the total time,
S=120025a4aS=192mph
Therefore, the correct option is option c.
Additional information:
Distance is a scalar quantity and it generally tells us how much ground has been covered by the object. In the other case, displacement is the shortest distance an object could travel between the start and the endpoint. As average speed relies on the average distance but not displacement, the average speed will come under scalar quantity. Whereas, the average velocity will be a vector as average displacement is used in the formula. Speed doesn’t have any direction and so the average speed too. Average velocity will always tell us about the direction in which the object is traveling.
Note: If the object travels a lot of distance and ends at the same point where it started, the average speed can be calculated but the average velocity of the object or any object in such condition is zero. If the endpoint and the start point of the object is the same, the displacement covered by the body is zero, which results in zero velocity, thus zero average velocity.
