Question

An aeroplane can carry a maximum of 200 passengers. A profit of Rs. 1000 is made on each executive class ticket and a profit of Rs. 600 is made on each economy class ticket. The airline reserves at least 20 seats for executive class. However, at least 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximize the profit for the airline. What is the maximum profit?
(A) 136000
(B) 1360000
(C) 13600
(D) 1360

Answer 1

Assume that the number of executive class and economy class passengers be $x$ and $y$ . As per the information provided, we have four constraints for $x$ and $y$ i.e., $x+y\le 200$ , $x\ge 20$ , $y\ge 4x$ , $x\ge 0$ and $y\ge 0$ . We have Profit = Rs. $1000x+600y$ . We have to maximize the profit. Obtain the coordinates of the corner points and check where the profit function is maximum.

Complete step by step answer:
First of all, let us assume that the number of executive class and economy class passengers be $x$ and $y$ .
The number of executive class passengers = $x$ ………………………………………….(1)
The number of economy class passengers = $y$ …………………………………………..(2)
The total number of passengers = $x+y$ ………………………………(3)
According to the question, we are given that the maximum number of passengers is 200 …………………………………………..(4)
Now, from equation (3) and equation (4), we get
$x+y\le 200$ ……………………………………………..(5)
It is also given that at least 20 seats are reserved for executive class ………………………………(6)
Now, from equation (1) and equation (6), we get
$x\ge 20$ ………………………………….(7)
It is also given that the number of the economy class should be at least 4 times the executive class ………………………………………..(8)
Now, from equation (1), equation (2), and equation (8), we get
$y\ge 4x$
$y-4x\ge 0$ ………………………………………….(9)
The profit on executive class = Rs. 1000 …………………………….(10)
The profit on economy class = Rs. 600 ………………………………(11)
From equation (1), equation (2), equation (10), and equation (11), we get
The total profit = Rs. $1000x+600y$ …………………………………..(12)
We are asked to calculate the maximum profit. That is, we have to maximize equation (12).
Maximize Profit = Rs. $1000x+600y$ with the following constraints,
$x+y\le 200$,

$x$	0	200
$y$	200	0

$x\ge 20$
$y-4x\ge 0$

$x$	0	20
$y$	0	80

Also, $x\ge 0$ and $y\ge 0$ (the number of tickets sold cannot be negative)
Now, on plotting the graph, we get

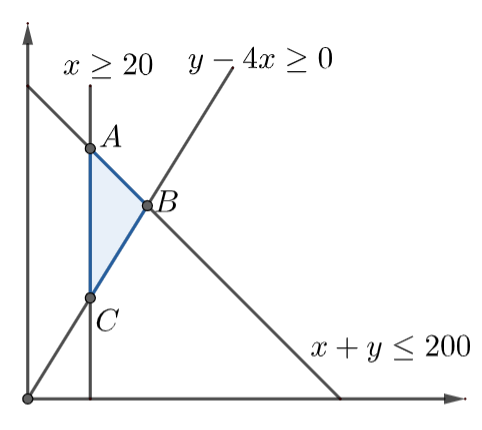
Point A is the intersection of the line $x=20$ and $x+y=200$ .
On solving $x=20$ and $x+y=200$ , we get
$x=20$ and $y=180$ .
So, point A is (20, 180) ……………………………………(13)
Similarly, point B is the intersection of the line $y-4x=0$ and $x+y=200$ .
On solving $y-4x=0$ and $x+y=200$ , we get
$x=40$ and $y=160$ .
So, point B is (40, 160) …………………………………………(14)
Similarly, point C is the intersection of the line $x=20$ and $y-4x=0$ .
On solving $x=20$ and $y-4x=0$ , we get
$x=20$ and $y=80$ .
So, point C is (20, 80) ……………………………………..(15)
Now, on putting the value of x and y from equation (13), equation (14), and equation (15) in equation (12), we get

Corner points	Profit = Rs. $1000x+600y$
A (20, 180)	128000
B (40, 160)	136000
C (20, 80)	68000

From the above table, it can be observed that the profit is maximum for point B (40, 160) and the maximum profit is Rs. 136000.

So, the correct answer is “Option A”.

Note: The best way to approach this type of question is to use linear programming that is, get all the constraints for $x$ and $y$ . Now, using the constraints, get all the coordinates of the points of intersection. Using the coordinates of the points of intersection of $x$ and $y$ maximize the required function.